Chapter 2.The Role of the Anamoly in Correcting Cosmological Models
Executive Summary
In this chapter we stress the importance of anamolous observations (one's that can not be easily explained by the model)as the prime motivators that lead to the development of new models. In essence, this is the process of science at work. When confronted with an anamoly you have three options:
The interplay between the above bulleted list is what drives the science/culture interface and understanding that dynamic is quite important to achieving science literacy. For instance, we could easily replace cosmology with global climate change and be confronted by the same list of 3 possibilities. |
The Nature of Science
To better articulate what is meant by a "scientific" model (as opposed to an arbitrary one) it is important to first define what elements consistute "Science". While each scientist might have their own grandiose definition of what consitutes science, for our purposes we can distill it down to 5 essentials:
- In science, ideas are supported by testable and verifiable experiments of observations.
- Science is a process or a procedure to investigate nature
- Scientific knowledge is not the same as possessing the Truth.
- Science seeks consistency between observations and models far more than it seeks complete explanations.
- Operationally, science usually procees by a method of empirical falsification.
However, the scientific method, as defined by the 5 elements above, as told to most students is rather far from the way in which real science is done by real people. There is no formulaic method that scientists follow to magically produce scientific results as if there was some cookbook approach to science --follow the recipe and bake a scientific cake. At its core the scientific method is a process that a) objectively investigates a phenomenon and b) attempts to produce a consistent explanation for the observations.
Science begins with an objective observation which is generally more difficult to achieve than is appreciated because of prior experiences and/or biases. For instance, when an adult looks at door, they see a door because their prior experienced has identified that object as a door. When a 2 year old looks at a door, they observe to be a rectangular object with a shiny thing on it. In other words, the adult has not observed the door; they have instead, interpreted the object as a door based on prior experience. The 2 year old, however, has made a genuine observation (even though they can not readily communicate that observation). So one needs to be aware of the important difference between observation and interpretation.
The second point about consistency is even more important. Science/ the scientific method is not a pathway to the TRUTH. Rather it is a methodology, which usually maps our more that is unknown about a subject, than ever becomes known about that subject. The best that science can ever do is to provide consistency between observations and experiments and some theory that describes the subject. Scientific knowledge is therefore imprecise, it can never provide a complete explanation of our observations (and we should never expect it to!).
The basic operatinal components of the "scientific" method can be summarized as follows:
- Observe some aspect of the universe
- Invent a tentative description, called a hypothesis, which is consistent with what you have observed.
- Use the hypothesis to make predictions. This is a key part of the process because it allows one to more forward.
- Test those predictions by experiments or further observations and modify the hypothesis in the light of your results.
- Repeat steps 3 and 4 until there are no discrepancies between theory and experiment and/or observation.
Please refer to this powerpoint "podcast" for a visualization of this process
The great advantage of the scientific method is that it, in principle, it is unbiased and theory goes where the data leads in order to best promote consistency. Yet most of you think that science is a way to find an "Answer" and that scientific inquiry always leads to the "Truth". An acceptable theory is one that provides a consistent explanation, without anomalies. But it is also clear that when more precise observations, enabled by new technology, are applied to the theory, inconsistencies usually arise because now the observations are able to probe and test the theory at deeper levels. That is generally the source of corrections to our various cosmological models.
The Geocentric Universe:
As mentioned in Chapter 1 - the Greek framework of Air, Earth, Fire and Water provided order to the Cosmos. In addition, since all that is observed or created could then be understood as the interaction between these primal forces. This was a highly deterministic Universe where the role of chance was essentially dismissed as being important. This is an unfortunate perception of nature, that randomness or chance is unimportant.
The first truly geometric description of the Universe was provide by Anaximander cira 450 BC. Its a quite unwiedly model that requires the earth to be a cylinder (apparantenly Anaximnander didn't get out much) but none the less it does provide an overall geometrical framework.

The next refinement is the perfect crystalline spheres of Aristotle's unchanging Universe intially set in motion about the Earth by the Prime Mover. Although this model is quite well accepted and mostly consistent with available naked eye observations, nevertheless even though there were observations that were in conflict with the basic model and include the following:
- Transient phenomena such as comets, novae, and variable stars were observed. This indicates that the Universe does change but the Arisoteleans attributed these tranient events to disturbances in the upper atmosphere of the Earth and not to things happening in the celestial realm.
- The fact that Venus (and Mercury) were never seen at midnight would require them to have "sub-orbits" about the Sun as the Sun revolved around the earth. This is shown below and note that Venus is postulated to be closer to the sun than Mercury.
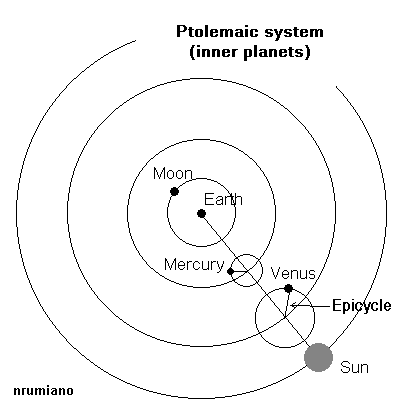
- The Aristotelian model makes the definite prediction that all the planets and stars should move in the same direction as the Crystalline Spheres upon which the planets and stars are fixed and therefore constrained to only rotate in one direction. However, at that time it was known that Mars would sometimes move in the opposite direction for a brief period of time (this is known as retrograde motion). This then is the anamoly in the Aristotelian model.
The retrograde motion of Mars was a serious challenge to the model and in fact, was sufficient to falsify it in favor of a simpler and more natural model. Indeed this backwards motion could be easily observed as every 780 days, Mars experiences an 83 day period of retrograde motion. Thus if you were plotting the position of Mars against a stellar reference system defined by various constellations, that position would appear to move backwards as shown in the following animation.

The retrograde period is centered around the time when Mars is in opposition - Mars is directly opposite the Sun such that the angle between Mars-Earth-Sun is 180 degrees.. Thus, this phenomena could be established as repeatable and realiable after only a decade's worth of observations.
Plato gave his students a major problem to work on: their task was to find a geometric explanation for the apparent motion of the planets, especially the strange retrograde motion. But the solution had to be consistent with the primary constraint at the time, namely the Earth should be at the unmoving center of the planet motions. One key observations is that near and during the time of retrograde motion, Mars appears significantly brighter in the sky than at other times. In the words of Plato
By the assumption of what uniform and orderly motions can the apparent motions of the planets be accounted for? That phrase is a very important one as scholars point out that the application of mathematics (which was the assigned student problem) to account for the apparent motions of the planets "by uniform and orderly motions" has been called "saving the phenomena"; in other words, saving the basic model of the unmoving Earth. The challange for the students would be to come up with a geometric scheme on how to combine various uniform circular motions in such a way that the resulting combinations matched the observe movement of the planets. There are basically two choices here: 1) and elaborate system designed to save the phenomena (which Ptolemy will produce) or 2) abandon the idea of the unmoving Earth altogether (which is what Aristarchus will do). There are no rewards for selecting option 2.
Option 1, however, had a tremendous number of attempts to fulfill but the contrivance that worked best was that of Ptolemy (circa 100-150 AD. Key to the Ptolemaic model is the use of epicycles in explaining planetary motions. These epicycles make a full description of a planetary orbit quite complicated as many parameters are required. This is shown in the figure below. In this figure the Earth is slightly offset from the center of the circle (C) defined by diameter AB. The planet, in orbit about the earth, moves on an epicycle centered on F which is "affixed" to the larger circle defined by diameter AB. The planet's movement on the epicycle could qualitatively account for observed retrograde motion. The final element, the equant represents a fixed point (Q) in which the epicycle center (F) rotates about. Since Q is offset from C, the distance between F and Q varies slightly throughout one orbital cycle like the distance between the Earth and the Planet.
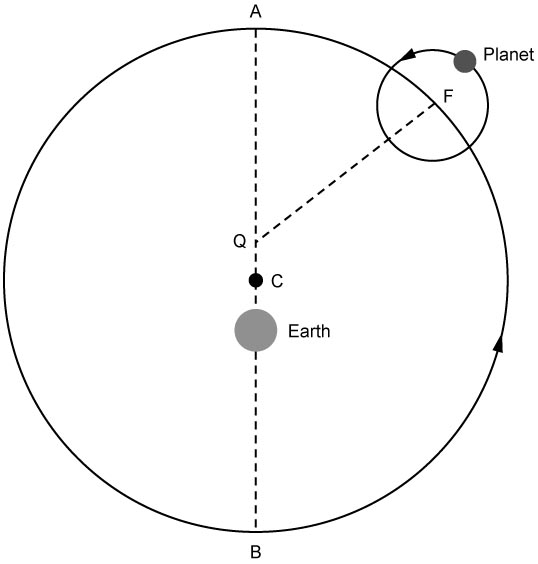
The use of these epicycles fully explains how a planet could appear to move backwards. If we refer to the Figure we see that the planet on the little wheel that rotates around point F oscillates between moving in the same direction as the big wheel (defined by the diameter AB ) and moving in the opposite direction. This would qualitatively explain why Mars would appear to move "backwards" at some times. Its not clear that this machinery correctly explains the duration over which Mars would behave in this way, but those observations were quite limited at the time.
While the Ptolemaic system is very cumbersome and complicated (and completely unnecessary) as far as its mechanical purpose as an astronomical clock, the model predicted the positions of the planets quite well to the naked eye accuracy of the time. Therefore a) it seemed to work, b) it keeps the Earth stationary and c) we still get to live in the center of the Universe. For these three reasons, this model will be accepted as the Truth until around 1500 AD.
Two important Early Geometric Measurements
Eratosthenes (220 B.C.) used a clever technique for estimating the size of the Earth. He knew that the Earth must be a sphere because of the shape of the shadow it periodically cast on the moon. Of course, a sphere is a prefect figure which was consistent with the important philosophy of perfection that was rampant at this time. Since there are 360 degrees in a sphere then the circumference of the earth can be estimated by determining how many kilometers are required to produce 1 degree of movement on the surface. Because the earth is tilted on its axis, the angle of the sun's rays with respect to any object depends on the latitude of that object. Similarly, the position of the Sun in the sky at a fixed time depends on the latitude. Eratosthenes determined that the angular difference between two cities (in what is now Egypt) Alexandria and Syene was about seven degrees based on the difference in the position of the Sun on the longest day of the year. This was determined by measuring shadow lengths at local noon in both locations. At Syene no shadow was cast, while at Alexendira that the shadow had an angle of 7 degrees with respect to the gnomon (a vertical stick you shove into the ground). This geometry is shown here:
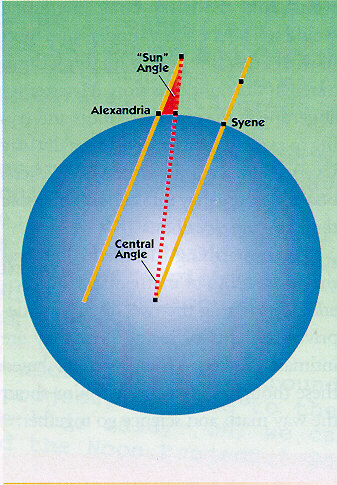
where the "Sun" angle measured at Alexendria is equivalent to the Central Angle as seen from the center of the Earth (because the light rays are coming into the Earth in a parallel manner). Because Alexendria and Syene are almost exactly at the same longtitude (i.e. Alexendria is almost due north from Syene) the central angle, 7 degrees, corresponds to the latitude seperation between these two locations. The linear distance between Alexandria and Syene was approximately 800 kilometers (which could be determined simply by walking between the two locations and carefully noting your distance over the course of an approximately 1 month journey) . Well, if 7 degrees corresponds to 800 kilometers of surface distance, then, since 7 degrees is 7/360 = .01944 (about 2%) of the circumference of the earth then the physical value (in kilometers) of the circumference must be 800/.01944 = 41143 km. This value is within 1% of the correct diameter.
A second set of important geometrical observations were made by Aristarchus (310-230 BC). Aristarchus developed methods to measure the relative sizes and distances of the Sun and the Moon. Even though his measurements are wrong, he does correctly conclude that the Sun must be much bigger than the moon and that the Earth and the moon are roughly the same size therefore the Earth must go around the sun (whoa, say it ain't so), the larger of the three objects. Thus, there is a correct heliocentric model that has been developed and "published" so others know about it. Under the heliocentric model proposed by Aristarchus the observed retrograde motion of Mars is a natural consequence of the Earth-Mars relative motion as Earth periodically "overtakes" Mars (when Mars is at opposition) in their mutual orbits. Thus Earth approaches Mars, reaches it, and then moves away from Mars. From out point of view (on Earth), Mars would therefore appear to be moving away from us. The two figures below summarize this situation.
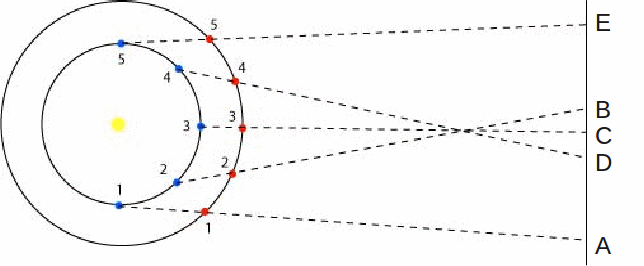
When the Earth is at position 2 it projects to position B on the plane of the sky. In this case its moving towards Mars and catches up with it at position 3 (position C). As the Earth moves from position 3 to 4, it begins to move away from mars relative to the plane of the sky. Hence Mars would appear to move in the sky from position B to Position D as the Earth moves from position 2 to 4. By the time position 5 is reached, the angle between Earth and Mars and the plane of the flattens out and Mars again would appear to be moving normally on its way to position E. An important thing to notice about this solution to the retrograde motion of Mars is that it requires the Earth to be physically moving faster in its orbit about the Sun than Mars. During these ancient times, there was no understanding of forces and accelartion so the cause of this faster motion would remain quite mysterious and in part, this precludes this model from being accepted.
This heliocentric theory also provide a natural explanation for why Mercury and Venus were always observed to be in the general vicinity of the Sun. From the point of view of the Earth's external orbit with respect to Mercury and Venus, there is a maximum angular extent that, say, Venus, can ever be from the Sun. This maximum angular extent is known as greatest elongation and is shown below. In the case of Venus, 47 degress corresponds to about 3 hours of time (as, at the equator there are 360 degrees/24 hours of time = 15 degrees per hour when time is mapped onto degrees of rotation). Hence Venus can never be observed more than +/- 3 hours from either sunset or sunrise.
Aristarchus also noticed that when the moon is exactly half full, the Earth (E) - Sun (S) - Moon (M) angle must be exactly 90 degrees as shown below
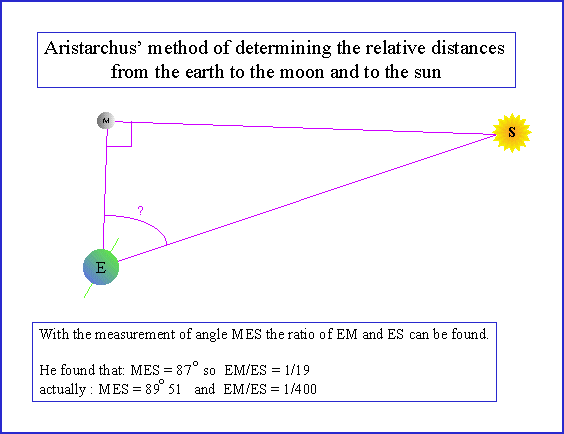
Therefore, thanks to Phythagorus, we know that a measurement of the angle M-E-S when the Moon is half full will give the ratio of the Earth-Moon distance to the Earth-Sun distance. From this Aristarchus derives a value of 19 to 1 as the ES/EM ratio. This is about 20 times too large but this is a difficult measurment to make as a)its hard to determine exact center lines to the moon and especially the Sun, b) refraction at sunset produces an artifical error, and c)it is hard to know when the moon is exactly at 1/2 phase. His measured angle was 87 degrees but the various errors involveconspire to prevent him from measuring the true angle or 89.85 degrees. Hence, this strategy, while sound, requires the ability to make very accurate measurements in order to reliably determine ES/EM.
Moreover, during a lunar eclipse (which happen relatively frequently) Aristarchus he measured the duration of time between the moment when the edge of the Moon first became eclisped and the moment when the Moon was first totally obscured. He also measured the duration of totality. Because he found the two times to be the same, he concluded that the width of the Earth's shadow at the distance where the Moon crosses it must be twice the diameter of the Moon. Therefore, the Moon must be 1/2 the size of the Earth (this is pretty close given that its hard to mesaure time vary accurately; the actual ratio is 0.271)
Finally, Aristarchus reasoned that since the Sun and the Moon have the same angular size (which is why there can be a total eclipse of the Sun), but the Sun is 19 times further (or so he thought), then the Sun must be 19 times bigger than the Moon or 9.5 times bigger than the Earth. Hence, in the mind of Aristarchus, the Sun was the dominant object in the Solar System but most others were unconvince. Nevertheless, Aristarchus serves as an important reminder that, although one's methods may be correct, if you don't have the instrumental precision to make the necessary measurements, its very difficult to make your model convincing. Indeed, had a telescope been invented at the time of Ptolemy, his model could easily be ruled out as the more precise telescopic measurement of the positions of the planets would be in noticeable disagreement with his model. In fact, this is exactly what Kepler will figure out from improved precision measurements of the position of mars, made over a 20 year period, by Tycho Brahe.
Moving Slowly to the Accepted Heliocentric Model
The Ptolemaic model would remain unchallenged (although there is evidence that heliocentrism was considered in the Arab world in the 8th and 9th centuries) until the mid 16th century, when Copernicus (1473-1543) proposed a profound paradigm shift which swept away the previously accepted cosmology. The paradigm was a simple one: The Sun was at the center of the solar system. The Geocentric cosmology of the ancients was now supplanted by the much more natural Heliocentric Cosmology of Aristarchus. Although history rightly identifies Copernicus as an important contributor there is another figure, Nicholas of Cusa who in 1440 wrote the following two pieces:
It is now evident that this earth really moves though to us it seems stationary. In fact, it is only by reference to something fixed that we detect the movement of anything. How would a person know that a ship was in movement, if, from the ship in the middle of the river, the banks were invisible to him and he was ignorant of the fact that water flows? Therein we have the reason why every man, whether he be on earth, in the sun or on another planet, always has the impression that all other things are in movement whilst he himself is in a sort of immovable centre; he will certainly always choose poles which will vary accordingly as his place of existence is the sun, the earth, the moon, Mars, etc. In consequence, there will be a machina mundi [scheme of the world/universe] whose centre, so to speak, is everywhere, whose circumference is nowhere, for God is its circumference and centre and He is everywhere and nowhere.
you will recognize that the art of calculating lacks precision, since it presupposes that the motion of all the other planets can be measured by reference to the motion of the sun. Even the ordering of the heavens --with respect to whatever kind of place or with respect to the risings and settings of the constellations or to the elevation of a pole and to things having to do with these-- it is not precisely knowable. Since no two places agree precisely in time and setting, it is evident that judgments about the stars are, in their specificity, far from precise
In these writings, Cusa is bringing up a principle which was not understood or appreciated before: All Motion is Relative.. This is a new (and quite correct) concept as all before had laboured under the notion that motion was absolute. But Cusa understands completely that motion is relative and therefore to properly define the position and motion of any object requires and agreed upon external reference system. Without such a system, there can be no accurate measurements of position and motion for any object.
We can illustrate the need for a reference system via the following example:
-
Alice and Bob are in an enclosed room and represent independent observers both seated in cushy seats and facing the way the arrows indicate.. Alice and Bob can't see each other becaue the room is very, very big. A grid of lines is painted on the floor of the room.
Alice posses the ball of wisdom that Bob would really like to get his hands on. Alice randomly throws the ball of wisdom in the enclosed room and it ends up at the position as shown in the figure below:
Without an agreed upon coordinate system we can imagine this kind of conversation (remember A and B are independent observers).
Bob to Alice (B to A): "Where's the ball?"
A: Uh, I don't know, its a bit to my left.
B: Huh, I don't see anything that is "a bit to my left."
A: Try your other left ...
B: Nothing there either
A: Maybe its behind you
B: I can't even see you, A, so what does "behind me", mean?
A: I don't know I can't see you.
B: Where's the damn Ball?
A: I already told you, its a little in front of me on my left.
B: What does "in front of you" mean?
A: I don't know, just come over here and I will show you.
B: I have no clue where you are Alice, how can I come over there if I don't know where "there" is.
A: Oh this is pointless, let me get out of my comfy chair and through the ball in your general direction.
B: But, Alice, you don't know where I am let alone what my general direction is.
A: Yes your right, it seems that you will never find the ball, hee, hee. It's really a wonderful ball.
B: Wait a minute, there are grid lines on this floor - tell me the location of the ball using grid units.
A: What's a grid unit?
B: One square on the floor is 1 grid unit.
A: How do I know that your squares are the same as mine?
B: You don't - we must assume that your Universe and my Universe are the same. if we don't then assume that then the ball of wisdom only exists in your Universe and not mine and that would be sad.
A: Okay then, the ball is 3 grids in front of me and 1 grid to my left. That locates it precisely.
B: There you go, using that "in front of me" stuff again. How does that help me?
A: Okay its in grid 17
B: What? - what the hell is a grid 17? Where's grid zero?
A: I don't know where grid Zero is .. what is grid zero? - do we need one?
B: Gee, Alice, I don't know if we need one either. This is impossible -- I am going to back to staring straight in front of me. Goodbye Alice.
- Some agreed upon grid has to be (0,0)
- Bob has to know what grid comprises his current location (i.e. some one needs to tell Bob where he is at or Bob needs to make some kind of external measurement to validate his position).
Note, as an added bonus, if Alice tells Bob what grid she is in, Bob can find Alice (provided she didn't move grids and didn't inform Bob).
So, without an agreed upon coordinate system, most measurments make no sense. This essential point was not realized by the Aristotelians. While Da Vinci thought about the need for a coordinate system, and Descartes will formalize this, it is really Nicholas of Cusa that emphasizes that all motion is relative to the coordinate system and hence position measurements of stars are indeed "far from precise".
With the advent of the printing press, around 1450, new ideas about the world, in principle, could reach a larger audience. While the Bible dominated the printed works of the presses in Europe, Copernicus's book De revolutionibus orbium coelestium, first published in 1543, was the second most printed work. The purpose of the book is to work out the motion of objects in the solar system, including the Earth, in full mathematical detail. Moreover, Copernicus uses equally spaced perfectly circular orbits between the planets and uses a mechanism similar to the concept of the Prime Mover to initiate motion.
The Copernicun model places the sun at the center of the solar system and all the planets orbit about it. Most importantly, Copernicus endows movement to the Earth. In fact, three kinds of movement:
- annual motion (orbit about the sun)
- daily rotation (around a tilted axis)
- axial wobble (changes the positions of fixed stars over thousands of years timescale)
Contemporary criticism of this model centered mostly around the necessity of the moving Earth in this model. This criticism is best summarize in the sharp comments made by French philopsher Jean Bodin in 1506:
No one who is in his right mind or who has had the slightest training in the physical sciences will ever believe that the dense and solid earth with its heaviness and weight simultaneously moves up and down, about its own center, and around the sun, while performing a libration (oscillation around an axis)
The instance on keeping all the orbits as perfect circles resulted in a model that was every bit as complicated as that of Ptolemy. This can be seen from Copernicus's own words:
We must however confess that these movements are circular or are composed of many circular movements, in that they maintain these irregularities in accordance with a constant law and with fixed periodic returns: and that could not take place, if they were not circular. For it is only the circle which can bring back what is past and over with; and in this way, for example, the sun by a movement composed of circular movements brings back to us the inequality of days and nights and the four seasons of the year. Many movements are recognized in that movement, since it is impossible that a simple heavenly body should be moved irregularly by a single sphere. For that would have to take place either on account of the inconstancy of the motor virtue -- whether by reason of an extrinsic cause or its intrinsic nature -- or on account of the inequality between it and the moved body. But since the mind shudders at either of these suppositions, and since it is quite unfitting to suppose that such a state of affairs exists among things which are established in the best system, it is agreed that their regular movements appear to us as irregular, whether on account of their circles having different poles or even because the earth is not at the center of the circles in which they revolve.
As can sort of be read above (although personally, my mind remains shuddered about reading this) there is a diffculty of adquately accounting for the changing length of the day (the amount of time the Sun is above horizon). These difficulties also exist in the Ptolemaic model. Their root cuase is the assumption that orbits are circular. They are not, as Kepler will shortly reveal.
Finally, Andreas Osiander, an ordained Priest, oversaw the publication of De revolutionibus orbium coelestium and added an unsigned preface explaining that the model described in the book was not intended as a description of the way the Universe really is, but as a mathematical device to simplify calculations involving the movement of planets. In other words, the model was not real - it's just a device. We will see a similar sentiment expressed later when it comes to Galileo's telescope.
For it is the job of the astronomer to use painstaking and skilled observation in gathering together the history of the celestial movements, and then -- since he cannot by any line of reasoning reach the true causes of these movements -- to think up or construct whatever causes or hypotheses he pleases such that, by the assumption of these causes, those same movements can be calculated from the principles of geometry for the past and for the future too.
But since for one and the same movement varying hypotheses are proposed from time to time, as eccentricity or epicycle for the movemenet of the sun, the astronomer much prefers to take the one which is easiest to grasp. Maybe the philosopher demands probability instead; but neither of them will grasp anything certain or hand it on, unless it has been divinely revealed to him. Therefore let us permit these new hypotheses to make a public appearance among old ones which are themselves no more probable, especially since they are wonderful and easy and bring with them a vast storehouse of learned observations. And as far as hypotheses go, let no one expect anything in the way of certainty from astronomy, since astronomy can offer us nothing certain, lest, if anyone take as true that which has been constructed for another use, he go away from this discipline a bigger fool than when he came to it. Farewell.
Attemped Confirmation of the Heliocentric Model
Tycho Brahe (1546-1601) realized that it was possible to actually prove that the Earth revolved around the Sun if the stars are a distant fixed background. The method is known as stellar parallax which is the reflection of the annual motion of the Earth around the Sun as measured against the fixed background of stars. The principle of stellar parallax is shown in Figure below:
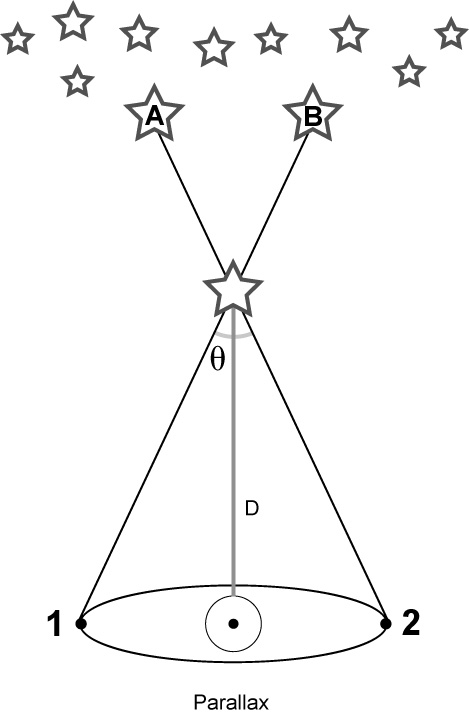
Figure 1.3 Schematic Representation of stellar Parallax. Distant stars act as a fixed reference coordinate system. Nearby stars, when observed 6 months apart, will show a small movement with respect to the background of fixed stars. At position 1, the nearby star would be viewed against a background that contained star B while 6 months later, at position 2, the nearby star would be viewed against a background that contained star A. When observations of a nearby star are made over a timescale of 6 months (over which the Earth has completed 1/2 of its orbit about the Sun), the position of that star appears to shift with respect to the fixed background of more distant stars. It was this shift that Tycho was determined to measure but he did not have a telescope. Instead, he made very accurate naked eye measurements. However, those naked eye observations were not sufficiently precise to measure the parallactic angle because, in reality, the stars are so far away that its impossible to measure that small of angle, even for the nearest star, with your naked eye.
While Tycho apparently considered this possibity, the required distances to the stars seemed absurd and so he abandoned this explanation for failing to detect parallaxy and instead concluded (erroneously) that the Heliocentric model must be incorrect. He then went on to develop his own solar system model (with the Earth firmly at the center) which was some kind of strange hybrid between the Ptolemaic Model and the model of Copernicus. A spectacular rendering of his model can be found in this Web Resource
Although Tycho drew the wrong set of conclusions based on his measurements, his naked eye observations of the position of Mars would turn out to have enormous value. This positional data was analyzed by Johannes Kepler (1571-1630) and this resulted in the formulation of Kepler's three laws of planetary motion. Kepler's improved geometric description of the solar system showed that:
- planetary orbits were not perfect circles but instead were ellipses
- planets must move faster when they are closer to the Sun
- the relative size scale
of the Solar System could be determined by measuring the orbital periods
of the planets. That is, there is a perfect relation between the orbital period of a planet and its distance from the sun. This perfect relationship is shown below:
The distance from the Sun to any object in the solar system could therefore be measured, relative to the Earth-Sun distance (which we define as 1 Astronomical Unit or 1 AU), simply by measuring its orbital period. For example, say we discover an Alien billboard in orbit about the sun which is asking Earthling's to become more sustainable and we measure its orbital period to be 1000 years. How far is that billboard away from the Sun. Kepler's third law tells us:
- P = 1000
 P2 = 1000 x 1000 = 1,000,000
P2 = 1000 x 1000 = 1,000,000
- A3 then equals 1,000,000
- The cube root of 1,000,000 = 100 AU.
- P = 1000
Kepler was able to discern the elliptical nature of the orbit of Mars because Tycho's naked eye measurements of the position of Mars over a 20 year time period were sufficient to show that the observed position did, in fact, disagree with the predicted position of Mars if its orbit was perfectly circular. In fact, the orbit of Mars deviates from circularity by about 9% where as the Earth deviates by only 3%. This is shown below:

Had the orbit of mars been as nearly circular as that of the Earth, Kepler would have not noticed its elliptical nature. As Kepler write:
And from this such small difference of eight minutes [of arc] it is clear why Ptolemy , since he was working with bisection [of the linear eccentricity], accepted a fixed equant point. ... For Ptolemy set out that he actually did not get below ten minutes [of arc], that is a sixth of And from this such small difference of eight minutes [of arc] it is clear why Ptolemy , since he was working with bisection [of the linear eccentricity], accepted a fixed equant point. ... For Ptolemy set out that he actually did not get below ten minutes [of arc], that is a sixth of a degree, in making observations. To us, on whom Divine benevolence has bestowed the most diligent of observers, Tycho Brahe, from whose observations this eight-minute error of Ptolemy's in regard to Mars is deduced, it is fitting that we accept with grateful minds this gift from God, and both acknowledge and build upon it. So let us work upon it so as to at last track down the real form of celestial motions (these arguments giving support to our belief that the assumptions are incorrect). This is the path I shall, in my own way, strike out in what follows. For if I thought the eight minutes in [ecliptic] longitude were unimportant, I could make a sufficient correction (by bisecting the [linear] eccentricity) to the hypothesis found in Chapter 16. Now, because they could not be disregarded, these eight minutes alone will lead us along a path to the reform of the whole of Astronomy, and they are the matter for a great part of this work.
The "reform of the whole of Astronomy" is referring to the abandonment that orbits are perfect circles.
Although Kepler did succeed in providing a "correct" model of the Solar System, there was no physics in it. All was empirical. While empirical models clearly have some value, they are ultimately unsatisfying as we have a strong desire to understand the reasons that the empirical model works. Without the underlying foundation there is no physical description and the Universe can appear to be ad hoc and capricious (i.e. what guarantee is there that Kepler's empirical laws apply to other solar systems?). Perhaps the elliptical orbit device used by Kepler is just another kind of epicycle?
Galileo Supports the Heliocentric Model
When Galileo first pointed his telescope at Jupiter he observed 4 points of light that changed their positions with time around the planet Jupiter on a nighly basis. He concluded that these were objects in orbit around Jupiter. Indeed, they were the 4 brightest moons of Jupiter, which are now commonly called the Galilean moons (Galileo himself called them the Medicea Siderea---the ``Medician Stars''). Galileo's observations were done over the course of 15 nights in January of 1610; two of which were cloudy. Clearly, the nightly changes in the positions of the moons relative to Jupiter was obvious for Galileo (and anyone else that observed the system) as he recorded the relative positions in his observing log book:
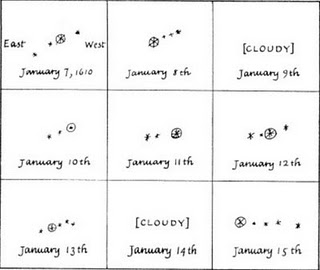
These new telescopic observations revealed that there were new things in the heavens that Aristotle and Ptolemy had known nothing about. The observations of the moon system of Jupiter clearly showed that more than one center of revolution can exist in the Universe (as suggested earlier by Cusa).Furthermore, they demonstrated that a planet could have moons circling it that would not be left behind as the planet moved around its orbit. One of the arguments against the Copernican system (and the original heliocentric idea of Aristarchus) had been that if the moon were in orbit around the Earth and the Earth in orbit around the Sun, the Earth would leave the Moon behind as it moved around its orbit.
However, the telescope is a new device that extends one's senses. But can it be trusted. One very prominent scientist of the time, Francisco Sizzi readily dismissed the importance of Galileo's disovery as follows:
Jupiter's moons are invisible to the naked eye and therefore can have no influence on the Earth, and therefore would be useless, and therefore do not exist.
Is this an absurd statement? Probably. But, it does raise the issue of independent verification. Afterall, how to you know that the instrument Galileo made is not a kalediscope, producing its own reality that has nothing to do with physical reality? It's annoying question - we will return to it later in the quantum mechinical framework. Of course, this statement is also relevant to the fact that wherever Galileo pointed his telescope he saw many more stars in it, than could be seen with the naked eye. Are those stars real? Can there truly be that many more objects in the Universe that we are unaware of? If there exists things in the Universe that we are unaware of, how can we ever be sure that our models are correct - well you can't ever be sure.
Newton Removes the Epicycle
Just like Aristarchus, Kepler, in the form of his second law, empricially knows that a planet moves faster when it gets closer to the Sun. But how can this occur? The planet is not touching the Sun. How does the Sun instruct the planet to move faster when it gets closer to it? This is indeed mysterious.Fortunately, Isaac Newton (1642-1727) was able to provide the foundation. Newton postulated that there was an attractive force between the Sun and the planets that had to account for Kepler's third law. Knowing that the Kepler's second and third laws meant that the orbital velocity of a planet must be a function of distance from the Sun, Newton deduced the functional form of the gravitational force law that would be required to reproduce these laws. As Newton was able to show, Kepler's third law requires that the gravitational force between two objects decrease as the inverse square of their distances.
We can derive Kepler's Third Law from Newton's equations as follows:
Step 1: Assume that M1 is a small mass in a circular orbit about a much larger mass M2 . We can write down the Force law on M1 using Newton's formulations: 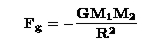
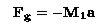
Step 2: Combining terms yields:
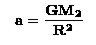
Step 3: In an orbit governed by a central force, the centripetal acceleration, a is given by:

Step 4: For a circular orbit, the circular velocity, Vc is the total distance traveled (the circumference of the circle) divided by the orbital period, P or Vc = 2p R/P which then yields:

The genius of Newton was his ability to use calculus and coordinate transformations to reveal the underlying physics. That is beyond the scope of this book. The point of this derivation was to show that only the R-2 force law can yield Kepler's Third Law. No other force law will work. If this gravitional force law is universal then Kepler's laws must also be universal. This would later be verified thorugh direct observations made by Herschel about 150 years later.
Newton's formulation of gravity allows Kepler's laws to become natural, which signifies the arrival of the first physical cosmology. The need for epicycles to make the model work is now gone (although the need will come back in a couple of hundred years). It would seem we have arrived at the "Truth" as Newton's laws precisely explain all of the observed motions of the planets.
But how big is the Universe?
The size scale of the Universe is always set by the most distant object whose distance you can realiably measure. At the time of Newton, this criterion was met by Saturn. At this time, the nature of stars was completely unknown but Galileos qualitative observations of many more stars seen through the telescope than can be seen with the naked eye is suggestive of a big Universe. But Galileo's telescope was a pipsqueak, a dinkly little 2.5 inch lense. William Herschel (1738-1822) improved upon this considerably by producing a 50 inch telescope to make his naked eye observations. This telescope could therefore see objects that were 400 times fainter than Galileo. Not only that, he also discovered the planet Uranus (in 1781) and now the Solar System has gotten approximately 2 times bigger than when Saturn was the most distant known planet.
When Herschel looked through the eye piece hey saw a vast universe full of very faint stars and produced extensive maps of the positions and brightnesses of stars. He also discovered many double stars (two stars in orbit about one another) from which he made very careful observations of orbital periods and discovered that the orbits objeyed Kepler's laws. Wow! Direct, observational confirmation of universality!
From Herschel's catalog, the first accurate stellar parallax measurement of 0.32 seconds of arc for the star 61 Cygni was published by the F.W. Bessel in 1838. This was followed in 1839 by Thomas Henderson's measurement of about 1 arc-second for Alpha Centauri and the 1840 measurement of Alpha Lyrae (Vega) at 0.26 arcseconds. Recall that 1 parsec is the distance a star would have to be at to have a parallactic angle of 1 arcsecond. This distance is equivalent to 3.26 light years. By 1840, it became clear that even the closest stars were more than one million times farther away than our Sun.
Indeed, by 1840 we have three new problems in the Universe that now may require their own epicycles to fix:
- What powers an object such that it can be still seen at these incredible distances of a few light years. Note that the distance from the Sun to Uranus is about 3 light hours ?
- Detailed observations of the orbit of Uranus showed that its elliptical orbit about the Sun was, in fact, not obeying Newton's Laws. So here we have another orbital anamoly.
- By 1859, detailed observations of the orbit of Mercury also showed that it did not conform to Newton's Laws. Oh my? Could Newton be incorrect?
Summary
In this chapter we have followed the evolution of cosmological model making over many centuries. A cosmology is a set of grand ideas and precepts about the way the Universe works. As such, cosmological ideas evolve directly in response to new data and new questions. The key components of this evolution are the following: - Models are ultimately derived from observations which are
made about the physical world.
- At any given time in history, people believe their cosmological
model of the day to be the correct one.
- The First "Scientific" Cosmology explicitly incorporated the use of
mathematics and geometry.
Rooted in observations of the relative
motion of the stars and planets in the sky, this cosmology culminated
in the Crystalline Sphere Universe of Aristotle. The chief features
of this Universe were a) it was finite in extent and b) the Earth
was at the center. The Universe of Aristotle was a perfect and
unchanging place, and there was little room for imagination.
- The Crystalline Sphere Universe made the prediction that
the planets and stars should all revolve in the same direction. However,
Mars was observed to occasionally move in the opposite direction.
To account for this motion and to preserve the Crystalline Sphere model,
Ptolemy built an elaborate system of orbital mechanics where planets
were affixed to a series of "wheels" and epicycles. This
cumbersome machinery allowed for retrograde motion and therefore allowed
for the Earth to remain at the center of the Cosmos. This model stood
for 1700 years.
- Copernicus, perhaps based on the earlier ideas of Cardinal
Nicholas of Cusa, suggested that the Sun was the center of the
Solar System and the Earth orbited about it. This heliocentric
cosmology was supported by the observations Galileo made of the moons
of Jupiter. In this mini-solar system Galileo observed small objects
in orbit about a larger object.
- Tycho attempted to prove the Earth was in orbit about the
Sun by measuring the predicted stellar parallax. However, his naked
eye observations did not have the precision necessary to make the
measurement. Rather than considering that alternative, Tycho declared
the heliocentric model to be false.
- Kepler used Tycho's observations of the position of Mars to
develop his three empirical laws of planetary orbits. Embodied in those
laws was the notion that a planet had to move faster when it was
closer to the sun but could give no explanation for this behavior.
- Galileo develops a new cosmological instrument and discovers that there is a lot of stuff in the Universe that was previously unknown.
- Newton established the dynamical basis for Kepler's
Laws by postulating the existence of an attractive force, gravity,
whose magnitude depended on the inverse square of the distance between
two objects with mass.
- Herschel cataloged the positions of stars to help map out
the structure of the Galaxy. In 1839/40 the first credible stellar
parallax measurements were made of some stars in this catalog. These
measurements showed that the stars had to be many millions of times
farther away from the Earth as our Sun was. The source of the energy
that could sustain such incredible brightnesses was unknown until
the early 20th century.
- With more precise observations, new anamolies have arisen. Science is hard.