Chapter 3. Wait, the Universe is Expanding? Gravity is Curvature? The Universe is full of Dark Energy?
Executive Summary
In this chapter we will move from the mid-19th century rapidly into the foundations of our current cosmological model of an expanding Universe. We will be told directly that mass and energy are actually the same thing! We will also achieve a profound new understanding of Gravity and have our faith in the concept of "certainty" severely shaken by the discover of Quantum Mechanics and its various implications. We will become confused.Near the end of this chapter, we will be forced to introduce two new "epicycles" into our cosmology - namely that the observed motions of galaxies in the Universe will require something called Dark Matter and the overall large scale geometry of the Universe will require something called Dark Energy. These quantities are epicycles in the sense that, as of now, we have no confirmed physical verification that they exist yet we know that they must exist. |
Ignorance, Doubt and Assumption
By the end of Chapter 2 we had made it to 1840 with the discovery of stellar parallax and correspondinly ridiculously large distances to the stars.. At this point, it is useful to introduce a device, similar to the Evil Genuis device of Descartes, known as the Random Alien Test (or RAT). Under the RAT device, an alien spontaneously appears and asks random planetary inhabitants basic knowledge questions about the Universe that any "intelligent civilization" would know. So, in 1840 the RAT question would be:
- What is the energy source of the stars?
and no one on Earth knows the answer thus distinguishing oursevles as a not very intelligent civilization.
Now if the RAT were introduced again in 1860, two more questions could be added to the exam:
- What is the mechanism that actually drives Darwian evolution?
- How come Mercury is disobeying Newton's Laws?
And for those of you wondering about the Evil Genius device, its really quite clever and comes into play when Descartes considers how reality can be best measured. In other words, at any given time, how do you know that there is not an Evil Genius running around doing arbitrary things to the Universe? If you can't rule out the presence of the Evil Genius in some experiment or observation, then you must doubt the results from that experiment or observation. Hence doubt is a necessary part of the scientific process. As semi-articulated by Descarets:
-
The first precept was never to accept a thing as true until I knew it as such without a single doubt
If you would be a real seeker after truth, it is necessary that at least once in your life you doubt, as far as possible, all things.
An important assumption in making a Cosmological model is The Cosmological Principle which asserts that the Universe must be homogeneous and isotropic. Put another way, the Cosmological Principle holds that the Universe is not arbitrary and, hence, any local physics that is observed must also exist on larger scales. Thus, Newton's formulation of gravity should be universal in its application. Herschels observations of the motions of double stars provide a direct confirmation of this universailty. Gravity should not behave differently on the Earth or in the Solar System as it would at any other location in the Universe. This cosmological principle, that the Universe is "everywhere the same", is clearly strongly implied in the writings of Cusa as well.
Anamolous motion of Uranus and Mercury
The planet Uranus was discovered in 1781 by Herschel. With this discovery, astronomers were eager to determine the orbital period of Uranus to determine its distance, using Kepler's third law. A reliable determination of an elliptical orbit can be acquired after observing about 1/2 an orbit. For the case of Uranus, the orbital period is 84 years so Uranus would have to be observed for 40-45 years to determine the orbital period and hence orbital distance of this newly discovered planet. In 1821 the first astronomical tables of the orbit of Uranus were published so that other astronomers could more easily locate it. As more and more observations were made, subsequent to 1821, it became apparent that the orbit of Uranus was not following an exact elliptical orbit as prescribed by Newton's laws; something "else" was pulling on Uranus. An unseen object was perturbing the orbit of Uranus causing it to deviate from Newton's laws. Ah ha, our first hints at dark Matter, in circa 1835!.
The most reasonable assumption for the origin of the irregular orbit of Uranus was that it was also being effected by another, nearby object, also in orbit about the Sun. Assuming that Newton's laws held for the orbit of the perturber, efforts in both England (John Adams) and France (Le Verrier) were then underway to calculate the orbit of the pertuber, based on its influence on the orbit of Uranus. After about a decade of work, both Adams and Le Verrier calculations offered a good predicted position for the perturbing object. On September 24, 1846, the planet Neptune was unambiguosly discovered at precisely the predicted location. Of course, Neptune is not dark matter, but the method of discovery showed the precise mathematical nature of Newton's laws - they really do work!
Not long after the discovery of Neptune, it was confirmed, in 1859, that the orbit of Mercury, in fact, also did not correspond to Newton's laws. However, unlike the case of Neptune, Le Verrier was able to conclusively show that the irregular orbit of Mercury was not caused by pertubations of the known planets. He then postulated the existence of another unseen planet with an orbit interior to Mercury. This hypothetical planet was christend as Vulcan and many observatories attempted to detect it and many false detections were announced, since, much like the dark matter problem of today, everyone assumed that Vulcan had to exist becasue the same techniques were used to succesfully detect Nepture.
Of course, observing a planet with an orbit that is inside of Mercury's is very difficult since that planet would always be near the sun. So the telscope had to be pointed near the Sun at all times, and the sky therefore could never be dark. Many of the false detections originated from trying to observe the transit of Vulcan across the Sun and mistaking a transit with round sun spots. After about 50 years of searching, without a detection, the existence of Vulcan was now seriously doubted leaving the issue of the perturbed orbit of Mercury, unresolved.
Curved Space-Time
A logical next step in the resolution of the orbit of Mercury is to ask, is there something special about Mercury that is not shared by the other planets. Well, yes, Mercury is the closest planet to the Sun so perhaps gravity behaves differently near the Sun than it does far from the Sun. In Newtonian mechanics, this would not be allowed so perhaps Newton's theory is incomplete at some level. It turns out that Newton never explicitly considered the "shape" of spacetime but implicitly assumed that space is completely flat. The resolution of the positional discrepancy of Mercury requires that space be "curved" in the vicinity of Mercury so that Mercury orbits inside this curvature. Such an orbit will differ slightly from an orbit in purely flat space. This is shown in the figure below:

But, why would space be curved in the vicinity of Mercury? The answer lies in Mercury's proximity to the Sun. Einstein postulated that gravity is really the manifestation of curved space and that very massive objects cause a greater degree of curvature and hence have a greater gravitational influence. Mercury is sufficiently close to the Sun that it orbits in curved space. The rest of the planets are far enough away from the Sun that the degree of curvature caused by the mass of the Sun is negligible. While a full description of the General Theory of Relativity is well beyond our scope, we can summarize it qualitatively as follows:
.
Space communicates with matter and instructs it how to move
and, in turn, matter communicates with space and
instructs it how to curve
In this way, the distribution of mass determines the overall curvature of the Universe as well as the particular pathways that objects, including light, must follow. These concepts will be further elucidated below.
E=mc2 - So That is Why Stars Shine!
When considering all aspects of relativity, Einstein rapidly came to the conclusion that there is must be one reference frame in which all observers could agree that they were making the same measurments. In order for that reference frame to exist, it would be come necessary that the speed of information transmission in the Universe (e.g. the speed of light) would remain constant for all observers in the Universe whether they were in motion or not. In other words, the speed of light has to be independent of the motion of a source. For instance, a star that is 10 light years away would always take 10 years to transmit light to the observer independent of whether the star was moving towards or away from the observer. As a result of this requirement, Einstein was able to show an equivalence between energy and mass. Furthermore, in the right circumstances mass can be converted to energy and vice versa. Hence

specifies a fundamental condition of our Universe. Mass can be converted to energy and energy can be converted to mass. The process of mass conversion to energy is known as thermonuclear fusion and it requires very high temperatures. Fusion means the heavier elements are built up from light elements. Stars can easily achieve this due to their tremendous masses that require high temperatures for stabilization against gravitational collapse.
In a simplified view of a star:
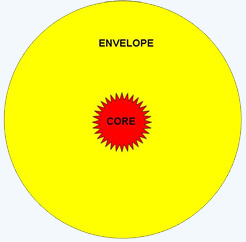
A ball of hydrogen collapses until pressure from the hot core stabilizes the star against further collapse. Each mass (which determines the amount of self-gravity) requires a unique core temperature for stabilization. Thus a 2 solar mass ball of hydrogen gas will require a higher core temperature for stabilization than a 1 solar mass ball of gas, which in turn is higher than for a 0.1 solar mass ball of gas. Any ball of gas larger than 0.1 solar masses will require a stabilization temperature that is sufficiently high (about 5 million degrees) that mass can, in fact, be directly converted into energy (we will see in Chapter 4 that this also occurs in the early Universe). At such high temperatures conditions are favorable for the onset of fusion and the generation of energy from mass conversion to energy. Remember that, the speed of light is a large number which means that c 2 i is absolutely gigantic. Thus, a relatively small amount of mass can provide a great deal of energy.
Another important consequence of E = mc2 is that photons, which have energy, E, also must have an energy-related mass. Therefore photons are subject to the same gravitional force as any other particle. In most cases, this gravitational force is so weak that the photon does not lose any of its energy. But, in regions of strong gravitational force (in the vincinity of massive objects) photons do loose some of their energy in order to escape from those regions.
The Geometry of the Universe
General relativity established the relation between mass and space. Mass causes a curvature in space time. The greater the mass, the greater the curvature. We can visualize this in the following figures which represent a 2D analog to the Universe. When there is no mass embedded in the surface the rubber sheet is not distorted and remains flat. Then we can see the effects of placing a larger mass on this rubber sheet. The large mass causes the surface to deform creating curvature in otherwise flat space. This curvature represents the gravitational potential well of that mass. Imagine rolling a ball bearing on this surface. If you gave the ball bearing insufficient energy and it found its way into a potential well, it would not come back out. It would stuck at the bottom of the well. This, in essence, is how gravity can capture material locally. Once mass is in a gravitational field (i.e. in a potential well), it has a tendency to stay there unless it can acquire enough energy to escape (climb out of the potential well)Finally we can see the effects of varying masses placed on the sheet. Each mass causes an indentation which represents its own gravitational potential well. You can see that the depth of the indentation is larger the more mass there is, indicating a higher degree of curvature at this location in the Universe than is seen around the smaller masses. Correspondingly,it would take even more energy for a particle to climb out of that potential well. If you imagine that you are a particle moving on this surface you can imagine moving in and out of different size potential wells. Between the wells space is flat, but while inside a well, space is locally curved by an amount directly proportional to the mass. Thus, the overall mass distribution of the Universe determines its geometry. This geometery in turn specifies the allowable pathways that matter and energy can take as they travel through the Universe.




The relation between energy and mass also has another fortunate consequence as it allows the Universe to be observable. Recall that the distribution of mass determines both the large and small scale geometry of the surface of the Universe.

|
Figure Ants in curved space time can only
communicate with one another via the blue path. The red path does
not follow the surface of the curved Universe.
|
The Dynamics of the Universe
When Newton discovered that gravity was an attractive force that effects all masses, he becamed concerned with the issue of why the Universe hasn't already collapsed. Afterall, if the Universe was infinite in age, as postulated by Arisotle, then all of the masses would have attrached each other into one giant mass and effectively the Universe would have collapsed. There are two ways out of this dilemma:
- The Universe is not infinitely old
- There is no net direction of gravity in the Universe so all the attractive forces balance out and there is no collapse.
That the Universe might not be infinite was first suggested in a series of arguments by Thomas Diggs and Kepler over the period 1590-1610. These arguments would later be refined by published in 1826 by a German astronomer named Olber and the argument goes by the buzzword phrase "Olber's Paradox" - although Olbers simply stole the idea (happens a lot in history). The basic argument is that if the Universe was infinite (with infinite mass in it) then it would contain and infinite number of stars. If there are an infinite numbers of stars (unifomrly distributed) then now matter where you looked in the sky, your line of site (no matter how narrow) would intersect one of these infinite numbers of stars such that the sky would never appear to be dark.

This argument is sufficiently convincing that by the time of Einstein, no one thought that the Universe could be infinite unless in an infinitely old Universe most all of the stars had burned out by now (and apparently had not reformed). That situation is very unlikely and implies also that humans had to come into existence at special time during this infinite lifetime of the Universe. To Einstein, the Universe was a finite and static place. Therefore, Newton's collapse dilemma re-emerges. Einstein's solution to this dilemma, however, was considerably more complex. In order to avoid universal collapse, Einstein postulated the existence of another field which acts as a long range repulsive force. This repulsive force completely balances the attractive force of gravity to keep the Universe static. Thus, by 1909 we had a model of the Universe that was similar in spirit to that of Aristotle. A finite Universe kept in balance, but this time instead of crystalline spheres providing the support, we had this peculiar other "force". We will give this other "force" a name later, but right now, by our previous historical logic, this looks very much like an epicycle.
In addition, the size scale of the Universe was also not well determined. While stars could not be observed with distances as large as 10,000 light years, all of those stars are contained within our Galaxy. It remains to me seen whether or not objects actually exist in the Universe that are at distances well beyond our galaxy (and hence would be extragalactic objects). In 1909, this is not known. A RAT question in 1909 might be:
- How Big is the Observable Universe?
The Discovery of Universal Expansion
By 1900, astronomical photography with telescopes had become fairly routine. In turn many objects described as "luminous spiral clouds of matter" had been discovered. The image below comes from 1910:

At this time, the physical nature of these "spiral nebulae" were completely unknown. A few years later, an astronomer named Vesto Slipher, using new equipment at the Lowell Observatory, started to take spectra of some of these spiral nebulae. A spectrograph is basically a camera with a prism in it that disperses the light into very narrow wavelength channels. A crude spectograph is simply a prism that breaks out white light into its component colors as shown below:
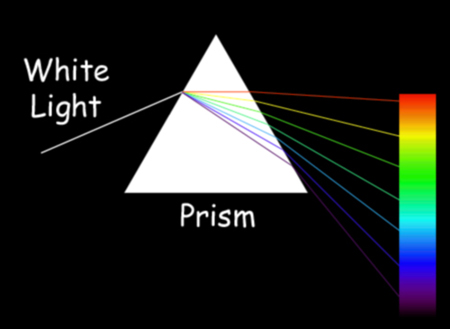
An astronomical spectrograph would say, break up the red part of the spectrum illustrated above, into a few hundred individual channels within that red part of the optical spectrum. This allows for a measurement of various spectral features of different elements that are due to atom-electron processes. The details of this process of atomic emission and absorption are not necessary to know for our purposes. What matters is how spectra can be used as a diagnostic process. For instance, the figure below shows the optical spectrum of the hydrogen atom as observed in the terrestrial lab. There are 4 bright features, called emission lines, that occur at specific wavelengths. For hydrogen this wavelengths are (from violet to red), 4101, 4340, 4861 and 6562 angstroms. Those wavelenghts correspond to specific electron energy levels within the hydrogen atom and those transistions are unique to the hydrogen atom. Each element has its own unique spectrum of atomic features (emission or absorption lines).
Now suppose that you put a source of hydrogen emission on a train and you took a spectrum that hydrgoen well it was on a train moving away from you. In this case, the observed wavelength of say the red Hydrogen emission line would not longer be at exactly 6562 angstroms, but it would be shifted towards a longer wavelength (a redshift) depending upon the velocity of the train away from you. Motion along your line of site is known as radial motion . If the radial motion of the train were towards you, you would observe the 6562 angstrom line shifted to a shorter wavelength (a blueshift). This shifting of the observed wavelengths or frequencies of spectral feature as a function of the motion of the source is known as the Doppler Effect which is illustrated below:

|
Figure 2.2 Schematic illustration
of the compression and/or stretching of light waves from a
moving source. Observer A would see a redshift while
Observer B would see a blueshift. The amount of shift depends
upon the velocity of the light source.
|
By 1914, Slipher had measured Doppler shifts for a sample of 15 spiral nebulae. Most all of those ojects exhibited a redshift (motion away from the observer) and the largest measured redshift was 1100 km/s. That large redshift is important because objects that are in our own Galaxy do not have velocities much larger than 300-400 km/s. The significance of this large redshift, however, eluded everyone at this time. In addition, the statisical result that most spiral nebulae showed redshifts instead of blueshifts was not well understood. In other words, the RAT shows up at the 1914 meeting of the American Astronomical Society, where Slipher first report the results, and asks the audience (all expert astronomers).
- What is the explanation for the observed Redshifts of Spiral Nebulae?
Mathematically, the amount that the light is shifted depends only on the radial velocity of the object. This shift is given by
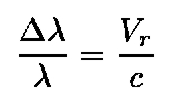
A galaxy with Vr (its radial velocity) of 3000 km/s will show a shift of 1%, as the speed of light is 300,000 km/s. Thus, a spectral line which has a rest wavelength of 6562 Angstroms would be shifted by 65 Angstroms to the red and be observed at a wavelength of 6627 Angstroms. By 1921 Slipher had measured as total of 41 Doppler shifts the largerst now being 1800 km/s. Still, the origin of this persistent motion away from the observe for these objects was not resolved.
At the time galaxy redshifts were first being measured, there was also a debate about the overall nature of these nebulae (galaxies). There existed two possibilities, either a) these nebulae were part of our own Galaxy and their redshifts were due to motion within the Galaxy (but redshifts larger than 500 km/s would be difficult to explain in this manner), or b) these nebulae were actually separate galaxies that lay at distances far beyond the dimensions of the Milky Way. Until there was a way to determine the distances to these nebulae, this debate does not have a satisfactory resolution.
This dilemma culminated in the Shapley-Curtis debate in 1920. The title of this debate was Scale of the Universe and like our ancient ancestors it represented humanity once again struggling to find its proper place in the Cosmos. At issue was the overall size of the Universe. Shapley argued that the spiral nebulae Hubble and others were measuring were just gas or dust clouds in our own Galaxy and that, therefore, the Milky Way was the Universe. Curtis, however, advanced the idea that these spiral nebulae were galaxies just like our own which indicated that the Universe consisted of a sea of individual galaxies. Each point of view had its merits and could be supported by the data on hand at the time. Inadequate or ambiguous data often is the reason for scientific debate and this is part of the scientific process. The debate usually ends when sufficiently good data arises to declare one side the winner. There was no winner in this debate, although Curtis would turn out to be right as evidenced a few years later.
The data that supported the position of Curtis would be published 5 years later, in 1925, by Edwin Hubble.This good data came in the form of Hubble's discovery of Cepheid variables in the Andromeda Nebula (M31) in 1923. Using the 100-inch Telescope at Mt. Wilson, Hubble took many photographic plates of M31 and observed some of the brighter stars to vary in brightness over time. By 1925, Hubble had sufficient data to show that these variable stars were just like the Cepheid variables seen previously in the Large Magellanic Cloud (LMC).
| Two views of the nearby Galaxy that Magellan first noticed in the Souther Hemisphere. The view on the left shows the stellar distribution of the older stars; the view on the right emphasizes the light from younger stars. The vast difference in appearance is a complicating factor in determining the actual distance and depth (along the line of site)of the LMC but this amounts to only a small correction in the distance to Andromeda. |
Cepheid variables exhibit a strong relationship between their instrinsic luminosity and their period of variation. This relationship is known as the Period-Luminosity (PL) relation and is shown below:

In the case of the longest period Cepheids (order 100 days) their luminosity is about 250,000 times brighter than our Sun which, in principle, allows them to be detected at very large distances. Since all of the observed Cepheids in the LMC were essentially at the same distance then the PL relation could be calibrated by obtaining the distance to the LMC by some means. Early attempts at measuring this distance, while somewhat inaccurate, were good enough for Hubble to make his important discovery. What Hubble noticed, after a few years of observations, was the the Cepheids in M31 exhibited the same slope of the PL for the LMC so he assumed he was observing the same phenomena (universality again). The only difference was that, on average, the Cepheids in M31 were 200-300 times fainter than those in the LMC.
Since the flux from an isotropic light source (like a star) diminishes with the square of the distance to the source, then for these Cepheids in M31 to appear ~ 250 times fainter than those in the LMC, the distance to M31 must be √ 250 ~ 16 times farther away from our Galaxy than the LMC is thus confirming that M31 is located about 2 million light years away. Earlier, during the 1920 debate, Shapely had estimate the size of our galaxy to be 50-100 thousand light years and thus M31 would be at least 20 Milky Way galaxy diameters away - making it truly an extragalactic object and confirming the position of Curtis.
Having now demonstrated that the spiral nebulae were indeed other galaxies, then their observed redshifts reflected some form of relative motion between the galaxies. But what could drive this relative motion? Over time, Hubble acquired spectra of fainter and smaller galaxies. He noticed that, in general, their observed redshifts were significantly larger than were observed for bigger and brighter galaxies. By assuming that all galaxies had the same physical size or were of the same physical brightness, Hubble concluded that the smaller and fainter galaxies appeared that way because they were farther away. Hence, Hubble used the apparent size or apparent brightness of a galaxy as a distance indicator
When Hubble then plotted the observed redshift versus the indicated distance he saw a correlation. Although the original data (from his 1929 paper) is quite noisy (see figure below) there is a tendency for the more distant galaxies (e.g. the galaxies of smallest angular sizes) to have larger redshifts than exhibited by the larger, nearby galaxies.

Since the observation of universal expansion is called the Hubble Law (and not the Slipher Law of the Lemaitre Law), then clearly Hubble won out. Before examining the implictions of Hubble's discovery we must return to Einstein and his Cosmological Constant. Einstein was forced, by logic and physical reasoning, to come up with the Cosmological Constant because he assumed that the Universe was static. With the discovery that the Universe was expanding (approximately 20 years after Einstein proposed his constant), there was no longer any need for the Cosmological Constant idea and Einstein characterized it's development as his "biggest blunder". However, as we will later see, our current preferred cosmological model now has the cosmological constant as its centerpiece.
That the Hubble Law indicates universal expansion can be shown as follows:
Vr = HoD
where Vr is the radial velocity away from the observer, Ho is a constant (called Hubble's constant), and D is the distance to the galaxy. This linear relation between Vr and D means the Universe is in a state of uniform expansion. The slope of this linear relation is the expansion rate or Ho.

|
Figure Schematic representation of
velocity-distance relation. Each of the 5 galaxies is separated
from another by a distance D and thus each galaxy
has a velocity with respect to one another of V .
No matter which galaxy your are located on, you recover the slope
of the dashed line. The case illustrated here is from the perspective
of an observer on Galaxy 1.
|
The Ant Universe
There is always a good deal of confusion that students have when it comes understanding the nature of the expanding Universe. A lot of miconcepts exist, ideas of explosions, and all of that - but most of these misconceptions can be cleared up with some thought experiements (or real ones if you can find some cooperate ants) involving the Ant universe.To start with, get a small bomb and place some ants on its surface (hint: use indestructible ants). Set the bomb off and notice what happens to the ants. The ants will fly radially away from the center of the bomb but they will be distributed on an ever expanding spherical shell. At no time will the ants become spread out in radial distance from the point of the initial explosion. Instead, they will will remain confined to the shell as it diffuses outwards. This is not what we observe for galaxies, as alluded to before. Galaxies, therefore, are not "flying" through the Universe as a consequence of some physical explosion.Next, get a balloon and inflate it about half way. Sprinkle some ants onto the surface of the balloon and continue to inflate it. Notice that while you are inflating the balloon the ants are walking randomly around its surface. Some will be walking towards each other and some away. There will be no well-defined correlation between the distance between any two ants and their relative motion. This again is not what we observe and indicates there is some controlling agent that is causing the relative motion between galaxies to depend on distance.
Finally, get some glue (super glue works best) and glue the ants to the balloon (this is actually quite hard to do unless you have a really good pair of tweezers). As you inflate the balloon you will notice that the ants are no longer moving with respect to their glue spots, from your reference frame as the inflator. The ants are stationary on the surface of the balloon but the separation between each ant is increasing as the surface of the balloon increases as a result of it being inflated. If you pick any one ant on the balloon, all the other ants appear to be moving away from that ant. It matters not which ant you pick as the Universe has its center everywhere (Cusa 1440). Hence, every ant believes they are in the center of the ant distribution (you can ask them) when in fact you know that there is no center because the ants are distributed on a surface. So what happens when you let the air out of the balloon? The ants all approach each other until they are all together (more or less) in one big ant glue-ball.
Now replace the ant's with galaxies and recognize that gravity is the "glue" that fixes the galaxies to the surface of the Universe. In the case of the Universe, this surface is a four dimensional spacetime surface which is embedded in some five dimensional volume. As this is rather difficult to draw on a two dimensional piece of paper, we use the analogy of the two dimensional balloon surface embedded in a three-dimensional volume. The key is to adopt the ant perspective. The ant is a two dimensional creature that really doesn't know it's on a surface. As we just saw above, the surface of the balloon has no center and the collapse of the balloon means the surface area has decreased (in principle, to zero).
In the case of our Universe, as the surface expands, the separation between all the galaxies increases and the observational manifestation of this is galaxy redshifts. This uniform expansion of the Universe makes a clear and important prediction. If galaxies are getting farther apart from each other due to the expansion of the surface, then in the past the galaxies were much closer to one another. Indeed, there must have even been a time when all the galaxies (all the matter) in the Universe were together in the same space at the same time. This means that the early Universe was a very small dense place and in a physical state well-removed from how it is observed to be today. So there you have it, an expanding universe with no cosmological contant that has a definite beginning when all matter was together at the same place at the same time. Say what? - isn't it simpler just to go back to Aristotle and call it good?
The Future of the Expanding Universe
The presence of matter in the Universe means that the expansion is steadily slowing down as the combined gravitational attraction of the matter acts to slow down the expansion. In fact, if there is sufficient mass in the Universe, the expansion will eventually slow down and cease, and the matter in the Universe will then attract into what is colloquially known as The Big Crunch. This condition is known as a closed Universe. Conversely, if there is insufficient matter in the Universe then the expansion will never stop, but merely slow down and asymptotically approach zero. This condition is known as an open Universe. A closed Universe offers us the possibility that the Universe can be reborn, expand and re-collapse in an infinite number of cycles. We are simply now in one of those cycles. The next cycle might produce a Universe with a different set of physics that might or might not allow for the development of intelligent life. In contrast, an open Universe has the dubious distinction of happening only once and then expanding forever, never to re-collapse and begin again. This naturally leads to the question "What happened before the Universe" - a question that can't be answered with our current knowledge.
The large scale geometry of the Universe is different whether it's open or closed. In the case of the closed Universe, the curvature is positive, much like a the surface of a basketball. If one draws a triangle on that surface the sum of the angles is greater than 180 degrees. In addition, two light rays which are initially emitted in parallel will eventually cross after they have traversed the curved surface. In the case of positive curvature, the surface is attached to itself and that is the sense of the term "closed". This closed surface will expand to some maximum radius before re-collapsing. An open Universe has negative curvature, which is can be represented by a saddle surface. In this case, parallel light rays will diverge, the sum of the angles of a triangle is less than 180 degrees and the surface does not "connect" to itself. Thus, the surface just keeps expanding and does not reach a maximum radius. The boundary between the open and closed Universes is a special case called a critical Universe in which space is perfectly flat on large scales. We will later see that flat space is one of the specific predictions of the inflationary theory for the origin of Universal expansion in which case the Universe has a very specific mass density. These open, closed and flat geometries are shown below. If we can find some way to measure the geometry of the Universe then we can determine its fate.

| Figure Schematic representations of the possible geometries of space time. These are two-dimensional analogs of curved space. In positively curved space the sum of the angles of a projected triangle on that surface is greater than 180 degrees while in negatively curved space the sum is less than 180 degrees. |
The Importance of Ho
Currently a lot of observational research is being devoted to determining the value of Hubble's constant (Ho). This constant specifies the current rate at which the Universe is expanding. One of the primary research missions of the Hubble Space Telescope is to provide a determination of this parameter to an accuracy of 10%. But why is such accuracy important? Let's begin by looking at the units of this equation:
- Vr
is a velocity which is units of length divided by
time (kilometers/second).
D is a length (kilometers).
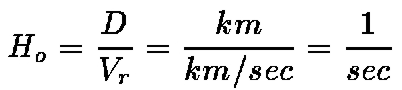
and see that Ho has units of inverse time. Hence, 1/Ho has units of time. The timescale given by Ho-1 is known as the expansion age of the Universe. This is not necessarily the same thing as the physical age but just represents how long the Universe has been expanding. The timescale Ho-1 is also strictly an upper limit to this age because the expansion rate is slowing down due to the gravitational attraction of all the matter. Thus, Ho was higher in the past than it is now. In fact, the timescale Ho-1 strictly holds for a massless Universe. If in fact there is enough mass density to close the Universe, then the expansion age is considerably lower and is equal to 2/3 Ho-1.
To further illustrate this, let's return to our ants that are still glued to the balloon. Let's suppose the balloon is attached to a pump which increases the radius of the balloon by one meter every day. If we wish to determine the expansion age of the balloon, all we have to do is measure its radius. For instance, if we measure a radius of 8 meters, then, given our knowledge of the expansion rate (1 meter per day) we know that the expansion age is 8 days. What the balloon (Universe) was doing prior to the expansion is not relevant to this calculation.
The second consequence of the expansion equation is the presence of a horizon. Special relativity fixes the maximum velocity of any object in the physical Universe to be c. Therefore if we replace Vr in the expansion equation by c we get
The meaning of cHo-1 is hopefully clear. This specifies the maximum distance between any two communicating objects on the surface of the Universe. Beyond this distance, objects would have to communicate with each other at a speed that would exceed c and that is forbidden. Thus cHo-1 defines our causal horizon and all observers are surrounded by such a horizon. This means there are actually two Universes: 1) the physical Universe and 2) the observable Universe. The observable Universe is that which exists within an observer's horizon. However, this does not mean that different observers see different Universes. Our assumptions about homogeneity and isotropy apply to all observers and means that the stuff beyond our horizon is the same stuff that we already know about.
Summary:
In this Chapter we have detailed how we arrived that the point of understandin that the Universe is not static, but instead is dynamically evolving through its expansion. Key milestones are the following:

