Darn Tutin' Pubs

Chapter 4. The Universe You Can't Build in the Lab: A Strange and Rapidly Evolving Environment. Executive Summary In this chapter we discuss the physical nature of the hot and very dense early Universe. Much of this physical nature is not adequately described by current physics which makes the initial conditions of the Universe completely unknown. We can start to sensibly describe the Universe after about 1/100 of second from its initial formation and subsequent expansion. Important concepts to understand include: The physics of the Universe as it progesses through various stages only depends on its temperature. The Universe goes from being radiation dominated to matter dominated. In the early stages, because there are 1 billion photons for every piece of matter, matter literally doesn't matter. E=mc2 comes into play in the very early universe through the process of pair production and pair annihiliation. As the Universe cools, only lighter and lighter particles can be produced via pair production. In the very early universe its is possible that very heavy, very exotic particles were produced; its unclear if any of those constinuents exist in the Universe now - if they do, they are the best candidates for dark matter. Helium formation in the early Universe was essential to preventing the neutrons from deacying away. The observed Helium abundance of the Universe is very consistent with the predicted abundance and this, along with expansion and the CMB, is one of the cornerstones of the big bang model. As long as the Universe is ionized, then free electrons will create a scattering network for the photons so the photons can not decouple from the matter. The longer this coupling time, the more the photons act to smooth out the distribution of matter and prevent the formation of galaxies or other structures. Expectations of a Hot Dense Early Universe By 1929 Hubble presented the bulk of the observational evidence for the expanding Universe. The uniform nature of the expansion leads to the unsettling conclusion that, if you run time backwards, there must have been some time when the Universe was a very small place, filled with a very large amount of matter. Hence, its density was, ludicrous. But what about the temperature of matter at ludicrous densities? The next step was the application of some simple thermodynamic models to the expanding Universe. To first order, the expanding Universe acts just like an expanding gas. As the gas expands to fill more volume it must cool. This is the thermodynamic concept of entropy, where the expanding gas becomes more disordered which requires a larger volume for it to fill. Well, the implication of an expanding and cooling gas is that, once up on a time, when the Universe was very young/small/dense, it also had to be very hot. In 1934, the physicist Tolman made a thermodynamic model of the Universe to predict that if the Universe has a temperature, then the pattern of radiation given off by that tamperature will have a thermal spectrum which will cool with time. This thermal spectrum will have the same characteristics as what we call blackbody radiation from stars. This means that if this radiation has always been present in the Universe and it has been cooling ever since, then the initial state of the Universe must have been very hot. In 1942, Chandrasekhar and Heinrich suggested that if the early Universe was in a state of thermal equilibrium, as argued by Tolman, with conditions of temperature near 10 billion K and density near 10 million grams per cubic cm, then helium could be created from the thermonuclear fusion of hydrogen. As we will see later, the formation of Helium is crucial to the preservation of neutrons and without Helium formation, the rest of the periodic table of elements would have never happened. The issue is, how long does the Universe stay in this state? The problem is that the postulated high density of the Universe at this time should cause it to rapidly collapse. To avoid this collapse, the expansion of the early Universe must have been very rapid and hence its temperature evolution was also rapid so the equilibrium state as envisioned above for the production of helium would not be possible. If the early Universe is governed by a state of rapid expansion and cooling then its very dynamic in nature. The physicist George Gamow explored this nature in a series of theoretical investigations in the 1940s. In so doing, Gamow postulated a very important condition that must have existed in the early Universe. At sufficiently high temperatures where the average energy of a photon would exceed the rest mass energy of a neutron, then it would not be possible for any atomic nuclei to exist. If one formed, it would be immediately photo-dissociated by one of these high energy photons. Hence, in this state, the Universe had to consist of a sea of elementary particles at very high temperature. As a result of this state, the current abundance of helium (the simplest element that contains neutrons) must be related to how much radiation was present. If too much radiation was present, helium might never have formed. Gamow used the estimated helium abundance of the Universe at that time to make a prediction about the level of radiation that now exists in the Universe. He predicted that the Universe should be filled with photons of characteristic wavelength a few millimeters if the expansion has been occurring for a few billion years. At the time this prediction was made, no technology existed to detected electromagnetic radiation at these wavelengths (i.e. the microwave part of the spectrum) and therefore perfoming a cosmological experiment to search for this predicted signal was impossible. This again illustrates the principle that advances in cosmological models (or really any science) often require having the right kind of detector available to test predictions. The Discovery of the Cosmic Microwave Background Gamow's 1948 prediction would have to wait until 1965 before it was roughly verified and even then, the discovery was accidental. However, this accidental discovery would later earn its discoverers' (Penzias and Wilson) a Nobel prize. This is also an illustration of the important role of chance in science. Often times true advancement in any field arises from accidental discoveries. Penzias and Wilson were scientists working at Bell labs at the time, exploring the newly opened world of Microwave communication. In order to determine the signal strength that would be necessary for good communication, it was important to measure the ambient background noise that the signal would have to compete against. So a Microwave telescope was fashioned and Penzias and Wilson set out to map out this noise. They immediately noticed that no matter where the telescope was pointed, microwave flux was received. Originally, they thought the source was terrestrial in origin but further observations showed that there wasn't any 24 hour modulation of the signal. This lead to one only conclusion. Since the flux density of microwave photons arriving at their millimeter receiver was independent of position on the sky, the source had to be cosmological in origin thus confirming Gamow's (who didn't receive the Nobel Prize) early prediction. This radiation is the Cosmic Microwave Background or CMB. In 1989, NASA launched the COBE satellite to explore the detailed temperature distribution of the CBR as Gamow had predicted a specific form. As shown below, that predicted form was strongly verified. The reason that the temperature of the CMB is currently 3K will be discussed in this chapter. 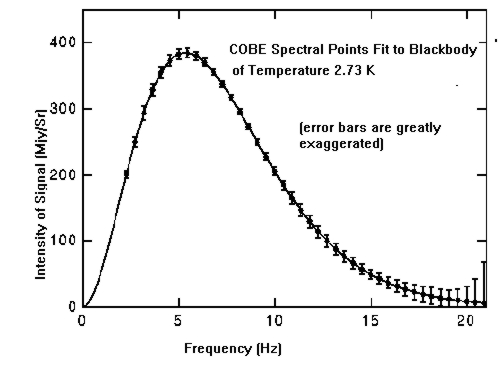Figure Blackbody fit to the 42 spectral data points obtained by the COBE satellite in 1990. The near perfect fit to the data indicates that the background radiation is like that of a blackbody, as predicted from the simple thermodynamic arguments made by Gamow. We thus have arrived at our second important cosmological observation - namely, the Universe is filled with a photon background whose energy today peaks in the Microwave part of the spectrum at a measured temperature of 2.74 +/- 0.02 K. This is one of the most precise cosmological measurements ever made and any cosmological model must be able to predict the existence of this radiation and its nearly perfect blackbody character. The energy of a photon is inversely proportional to its wavelength. Long wavelength photons, like those in radio waves, carry with them very little energy so they can pass through your body without any harmful side effects. Ultraviolet photons, however, have very shortwavelengths and thus high energy per photon. When these photons interact with your body, they have enough energy to disrupt some of your cells, thus giving you skin cancer. In the CMB, the average energy per photon depends only on the temperature of the radiation. Clearly as the Universe is expanding, the temperature is dropping and the average photon energy is decreasing (and shifting to longer wavelengths). This implies that at very early times in the Universe a) it was very hot and b) the average energy per photon was extremely large. Taking this to its logical extreme suggests that in the very early Universe, all of its energy wsa in the form of radiation and not matter. Radiation vs Matter Dominance The total gravitational energy density in the matter field is just related to the actual matter density (e.g. grams/cm3). As we will see later in this chapter, the total amount of matter in the Universe is fixed within its first second - after that the matter density is necessarily decreasing with time due to its expansion (fixed amount of mass in ever increasing volume), then the energy density of the matter is also decreasing. The energy density in the radiation field shows a different behavior with the expansion. The radiation energy density is equal to the product of the physical photon density times the average energy per photon. The energy per photon depends only on the temperature of the Universe which is cooling due to expansion. Under this simple thermodynamic condition, the radius of the expanding Universe is a proxy for temperature. Thus, not only does the number density of photons decrease with expansion but so does their average energy as the universe is cooling. If we consider a simple case where the radius, R, of a sphere inside the Universe is steadily increasing with time then the volume will increase as the radius cubed. Hence the number density (number of particles divided by the volume) of both the matter and the photons will scale as R-3 . However, in the case of the photons, the temperature also decreases with R and so their energy declines. 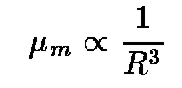This leads to the general condition that for the the matter and radiation energy densities, respectively. Figure Schematic representation of the faster fall off in the energy density of radiation compared to that of matter in and expanding and cooling Universe. The point where the two energy densities are equal is indicated. This point, called recombination. As graphically shown in the Figure above, this means that no matter what the initial state of the Universe is, the energy density in radiation (energy) decreases significantly faster with the expansion than the energy density of the matter. Therefore the Universe eventually must become matter dominated. In the case of our Universe, this takes about 100,000 years to occur. Prior to this time the Universe was radiation dominated as the energy density in the radiation field was greater than that in the matter field. The radiation dominated era leads to an immediate problem which is still no satisfactorily resolved. When the temperature of the Universe is high, the radiation pressure is also high and this radiation pressure can physically effect matter by a process known as radiation drag . As matter tries to clump due to gravity, the high radiation pressure intercedes and prevents the clumping. In fact, the radiation pressure is attempting to smooth out the distribution of matter as it couples to the matter via radiation drag and transfers momentum to the matter. This process is illustrated below: Figure 3.5 Visualization of two mass particles being bombarded by radiation and thus unable to gravitational "stick" together. The red arrows indicate the random directions of momentum the particles get when they are struck by the radiation. The arrows represent gravitational attraction. If the radiation pressure/momentum transfer would have been completely successful then the distribution of matter would be perfectly smooth and there would be no net gravity felt by one particle towards another (recall this was Newton's solution to the problem of the collapsing Universe). If there is no net gravity then there would be no galaxy formation (and you wouldn't be reading this sentence). The great challenge in understanding galaxy formation is understanding how density fluctuations can maintain their integrity and grow during the radiation dominated era of the Universe. As we will see, this may well demand the existence of dark matter. The Hot Big Bang Model On the basis of two fundamental observations, 1) the Universe is currently in a state of uniform expansion and 2) the Universe is filled with photons, we can construct our general cosmological model, which is known as the Hot Big Bang model. While the details of this model will be elucidated in the coming chapters, its synopsis is simple. The Universe started, for reasons unknown to us, in a very hot and dense state and has been expanding and cooling ever since. Within that synopsis this model can explain: The Origin of the CMB: This is a simple consequence of the Universe being filled with energy (photons) in its past. Once this energy/photon background is created, it cools with the expansion of the Universe and produces the background observed today. The Uniform Expansion of the Universe: By simple extrapolation to very small times, the currently observed expansion law, V=HD, must produce a situation where all the matter is concentrated into a small volume. At some point in this small volume, unknown physics initiated the expansion which caused the background radiation to continuously cool. Since the expansion has no preferred direction, the Universe is isotropic. This helps to explain the remarkable uniformity of the CMB - no matter where you look, you observe the same thing. This is a strong indication that the Universe is homogeneous as well. The Abundance of Light Elements: A hot dense early Universe would have gone through a period of nucleosynthesis that produced the light elements like Deuterium, Helium, and Lithium. The overall cosmic abundance of these elements is related to the relative matter and energy densities and the temperature of the Universe at early times. From this, predictions can be made concerning these abudances and those predictions generally agree with the available observations. As we will discuss later, the major unknown in the Big Bang model concerns the origin of galaxies and the development of the complex large scale structures that galaxies are embedded in. To understand this, we will have to appeal to the existence of dark matter. The presence of dark matter is not necessarily a general feature of Big Bang models and to account for it will require some modification known as the Inflationary paradigm. Well Then, Let's Begin at the Beginning The physics of the very early Universe is quite unknown. At these early times the Universe was in a very extreme state with a temperature of approximately 1032 K and a density of 1097 grams per cubic centimeter. These are absurd numbers of course and we have no real clue what kind of physics is occurring here nor even what the meaning of "space" is under such extreme conditions. Material properties like mass, volume density, etc have no meaning under these conditions. We do know that "ordinary" matter does not under these extreme conditions. Indeed, the most dense form of matter known is neutronium which has a density of 1014 grams per cubic centimeter, some 83 orders of magnitude less than the hypothetical density in this extreme state. Moreover, its completely unclear if any physical constants exist at this time. But if we pretend that the gravitational constant, G , the speed of light, c and the planck constant of quantum mechanics, ħ, all exist then we can take combinations of those three constants and turn them into units of Mass, Length and Time: But do those values mean anything or are they just nonsense? The Planck mass might seem to be a characteristic mass of the Universe at this time, but its both very small and very large. Its small in the absolute sense, but very large in the sense that its 1019 times the mass of a proton. In contrast, the characterstic length scale, the Planck length, is ridiculously small as its 10-18 times smaller than a proton. So even if you made a proton at this time, which you can't, but even if you did, then the proton would not come close to fitting in the length scale of the Universe and so the proton would be outside its own horizon and ... da ... my head just exploded. Bottom line - this state of ludicrous matter can not be adequately described given the physics that we know now. However, the Planck time might be interpreted as the time when the physical constants, by some mysterious process, actually come into being. That time, 10-43 seconds is indeed very early but physics prior to that time may well not have involved the physical constants as we know them today. Among the unknowns is whether or not quantum mechanics exists at these early times. If it did, there may have been important consequences since a fundamental tenet of Quantum Theory is known as the uncertainty principle may come into play. One of the variations of this principle tells us that we can never precisely know the energy state of a particular particle and the duration of that energy state. 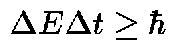In equation form, this is expressed as where ħ, (h-bar) is known as Planck's constant and is one of the fundamental constants of nature. 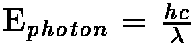This is the same constant that determines the energy of a photon: While Planck's constant is such a small value that the energy fluctuation equation above has no relevance in the macroscopic world, in the extremely early Universe, the time interval Dt could be arbitrarily small and hence the energy fluctuations DE could have been arbitrarily large. In this sense, the Universe has no choice but to happen as the energy fluctuations which produced it initially were naturally occurring. We don't know if this is the correct physical explanation or not. On the other hand, these quantum fluctuations in the early Universe certainly allow for the spontaneous creation of very massive hadronic pairs (because the energy levels are so high). Now its most likely that these heavy hadron + heavy anti-hadron particles just annihilated one another. However, there is a possibility that some small residue of very massive hadrons are left over. If so, they could be a major mass constituent in the Universe. These particles would be weakly interacting, meaning that they would not influence the dynamics of the early Universe or decay into smaller mass particles. Weakly interacting massive particles have been given the nickname WIMPs. If they really exist, there may be several of them whizzing through your body as you read this. There were other strange attributes of the Universe at this time. Easily the most theoretically spectacular possibility in this very early Universe involves the unification of the forces. For instance, at this time the gravitational force and the strong force have the same amplitude. Why is this so? As you know, the gravitational force law goes as R-2 but at very early times, R is extremely small (smaller than any particle) so the gravitational force is extremely large. This is a very strange physical regime which leads to the following theoretical possibilities: particle creation could come directly from the gravitational field. all of the Universe could be in the form of one particle but that particle would be indistinguishable from the gravitational field of the Universe. As the Universe is rapidly expanding, R is rapidly increasing and the gravitational energy is going down so that the gravitational force becomes much weaker than the strong force and the two become separate forces. By the end of this era, (10-11 seconds), a similar separation occurs between the electrostatic force and the weak force. Whenever these symmetric forces are decoupled the Universe is said to go through a phase transition. The symmetry breaking is done in a specific manner so that the forces have now separated and are defined by a characteristic ratio of their strengths. This defines the physics of our Universe. Much theoretical research is currently underway to better understand what causes the symmetry breaking and allows the forces to assume their characteristic values. Thus another question we are not allowed to ask is "how come gravity is as weak of force as it is?". We just don't know and moreover, not even the RAT knows. The Particle Physics Framework The basic framework for describing the thermal evolution of the Universe uses the principle of mass-energy equivalence, E = mc2 ; mass and energy are the same thing and can be converted from one form to the other. More specifically, the following reactions are possible in nature: photon + photon particle + antiparticle particle + anti-particle photon + photon The top reaction represents the case of pair production. In this situation, two energetic photons collide to produce a particle plus its anti-particle. The bottom reaction represents the case of particle annihilation in which a particle plus its anti-particle meet and annihilate one another to produce energy (photons). In the very early Universe, pair production and particle annihilation were occurring back and forth in equilibrium. The key point, however, is the following: since the temperature of the Universe is steadily falling (due to its expansion) and since the average photon energy depends on the temperature, then the average energy per photon declines as the Universe expands and cools. The kinds of particle/anti-particle pairs that can be created depends strictly on the photon energy. For instance, the neutron has a rest mass energy given by mnc2, where mn represents the mass of the neutron. A neutron plus anti-neutron can only be created if the initial energy of the photon is in excess of this rest-mass energy. This is why very high temperatures are required for pair-production and why, therefore, it can only occur in the very early Universe when the temperatures are much hotter than even those in the centers of stars (where pair production is not occurring). This leads to the general rule that if Ephoton < mpc2 then that photon has insufficient energy to spontaneously convert itself to a particle plus anti-particle of mass mp . What is a particle? Most of us are familiar with electrons, protons and neutrons as being what makes up atoms. But the world of particle physics is a bit more complex than this. However, the big unknown in all of particle physics is the process that gives the particles the masses they have. Thus, while it's possible to ask - "What is a proton?" and get a sensible answer, it is not possible to ask and answer "how come the mass of a proton is 1.67 x 10-24 grams?" In discussing the early Universe we will refer to the following kinds of particles: 1. Hadrons: A hadron is any particle which is subject to the strong force. Generally these are "heavy" particles (they have high rest mass energy). All hadrons are composed of quarks. Those hadrons that are composed of 3 quarks are called baryons. Protons and neutrons are familiar forms of baryons. Hadrons that are composed of two quarks are called mesons, which are a relatively exotic form of matter. 2. Leptons: These are light particles with low rest mass energy. They are not subject to the strong force and they are not composed of any sub-particles (there are no leptonic-quarks). A familiar example of a lepton is an electron. Another example is the neutrino, discussed below. The neutrino is a very important particle in the early Universe. 3. Quarks: These are the fundamental building blocks of hadronic matter. There are 6 known quarks: up,down,top.bottom,charm, and strange. A baryonic particle such as a neutron or a proton is made of 3 quarks. Some quarks carry charges, particularly the up and down quarks. An up quark has a charge of +2/3 while a down quark has a charge of -1/3. A baryonic configuration composed of two up quarks and one down quark would have a charge of +1. This configuration we call a proton. If one of the up quarks changes to a down quark, the charge will be 0. Now we have a neutron. In symbolic form this would be expressed as Proton = UUD Neutron = UDD The remarkable thing about quarks is that if you try to take one out of a proton, for instance, to produce a particle that therefore has only 2 quarks, you can't. The force that holds the quarks together increases with increasing distance of the quarks. As you try to pull the quarks apart, their attractive bond increases. This is essentially the way the strong force works. It's called the strong force because it's very strong and allows atomic nuclei to stay together. That is, a Carbon nucleus has 6 protons in it. Why doesn't the nucleus fragment because the 6 protons with like charges all repel one another? The answer is the strong force. If you can confine protons to small spacings the strong force takes over and binds them together. Separating them requires a great deal more energy than can be supplied by simple electrostatic repulsion. 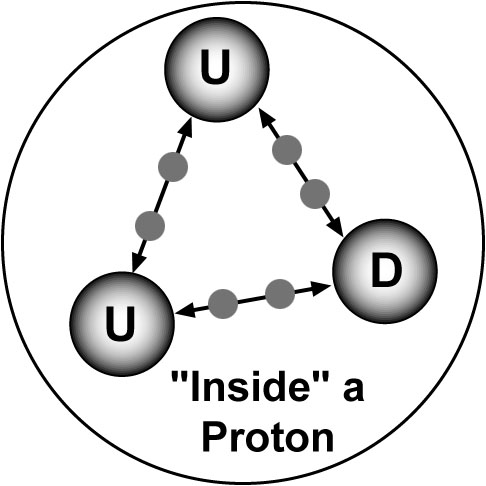Figure 3.2 Schematic representation of a proton with 2U quarks (U) and 1D quark (D). The force between the quarks is provided by the gluons, represented as solid black balls on the force line arrows. 4. Gluons: These are mysterious sub-particles that are the carriers of the force between the quarks. There name is apropro as they literally are the "glue" that holds quarks together. As you try to separate the quarks, thus separating the gluons, the force provided by the gluons strongly increases. This is schematically shown in Figure 3.2. 5. Neutrinos: These are very light particles but there are lots of them in the Universe. They carry no charge and have a very small cross section for interaction with other forms of matter. 6. Antimatter: Antimatter has all the properties of normal matter but they are just reversed. For example, an anti-electron has exactly the same mass as an electron but has positive charge (and hence is called a positron). Conservation Rules Although the early Universe may appear to be quite chaotic, with matter and energy constantly changing forms, there is a set of conservation laws that strictly govern the kind of particle interactions which can occur. Specifically, there are three things that need to be conserved in any particle interaction. These are Baryon Number Lepton Number Charge Number Whatever these three numbers were in any initial state, they must be the same in a final state. But what do these numbers represent? The Baryon number represents the initial baryon state. The units are +1, 0 , -1. A normal baryon, like a proton, would have a baryon number of +1. An anti-baryon would have a baryon number of -1. If the particle wasn't a baryon, its baryon number would be zero. Similar arguments hold for charge and lepton number. It is the strict adherence to these conservation rules that, for instance, allow for the spontaneous creation of some forms of antimatter during some particle decays, as in the case of neutrons which will decay with a 1/2 life of 900 seconds if they are not bound in an atomic nucleus. 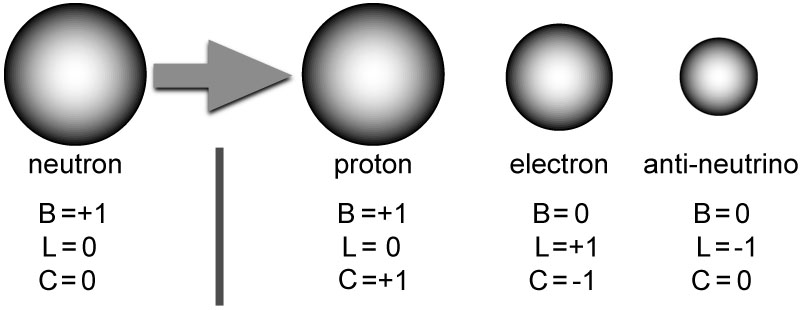Figure Visualization of the decay of the neutron to its 3 decay products. The baryon number, lepton number and charge for each particle is indicated. The decay path of the neutron is shown in the Figure. Let's examine each of the decay steps in detail. The initial state is just that of a neutron. A neutron has a baryon number of +1, a lepton number of 0 (because its not a lepton), and a charge number of 0 (its neutral). Whatever the form of the decay products, their total baryon, lepton and charge numbers must sum to the initial condition: Step 1: The neutron decays into a proton. The proton has baryon number = +1, lepton number = 0, and charge = +1. Now we have an immediate imbalance in the charge. Since conservation of charge is required (in order for the Universe to remain electrically neutral) we must balance this positive charge with a negative one. We cannot satisfy this condition with any negatively charged baryon because the total baryon number would be 2 instead of 1. Hence we require a negatively charged lepton. Step 2: An electron is a negatively charged lepton. It has baryon number = 0 (because it's not a baryon), lepton number = +1, and charge = -1. Now we have balanced the charge but to do so required the creation of a lepton. So now we have a lepton number of +1 on the decay side when the initial value was zero. Step 3: To satisfy the conservation laws, we need to create one more particle. This particle must have baryon number = 0 and charge =0. But it also must have lepton number = -1 and hence we must create anti-matter. A particle with these properties is the anti-neutrino. It is electrically neutral, it's not a baryon, but it is anti-matter and so its lepton number is -1. This is just one specific example but serves to illustrate the general rules. It also shows that the creation of anti-matter, within atomic nuclei processes, is required and natural. With our understanding of the conservation laws we can now see why a photon is a special particle. Consider when, say, a proton and an anti-proton annihilate. Since the anti -proton is a mirror image of the proton, then the combined baryon, lepton and charge numbers of the proton anti-proton pair must each be zero. Hence, the decay products must be 0. A photon is a unique particle in that it's neither a baryon or a lepton and it has no charge, so its value is zero. In that sense, a photon also acts as its own anti-particle. Because a photon is neither a baryon or a lepton it has no rest mass and hence can travel at the speed of light. Only photons or "photon-like" particles have this particular property. The Unknown Quark-Gluon Plasma When the Universe was very small, the quarks were very close together. Recall that the force between quarks , provided by the gluons, increases with increasing quark separation. When the quarks are very close to one another, the force drops dramatically. In fact, in this early Universe the quarks were so close to one another that no hadrons could exist. Hence, even though U and D quarks were present, they could not form a proton because the quarks cannot be bound together by the gluons and so the quarks had to be "free" in the sense that they were not contained in any hadron. At this point the Universe consists of a sea of high energy photons with individual quarks and gluons floating about. The basic condition for the free quark era is that the density of the Universe has to be in excess of nuclear densities (1014 grams per cubic centimeter). This condition is fulfilled when the Universe is less than 1 millionth of a second old. After this time, the expansion has lowered the density to below the nuclear density threshold and the quarks can now be assembled into hadrons. After this assembly, conventional physics more or less holds from here on out. Prior to this, the physics of this kind of free quark/gluon plasma is largely unknown. The important point here is that we have not yet created the basic elemenatry particles like protons and neutrons because the Universe is still too hot and dense for them to exist. The Unexplained Matter/Anti-Matter Asymmetry Between 10-11 and 10-2 seconds the Universe continues to cool rapidly. The reaction rate (the conversion of energy into mass and the annihilation of matter anti-matter pairs) was so large that the Universe was governed by a statistical process known as thermodynamic equilibrium. Under conditions of thermodynamic equilibrium the only thing that matters is the temperature. Hence, the conditions at any one time in the early Universe do not depend on the conditions that happened just before that time. The only thing that determines the physics is the temperature at a particular epoch. Under these conditions of thermal equilibrium, equal amounts of matter and anti-matter should be present at all times, buy yet only matter exists in the Universe. What happened? Where did the equal amounts of anti-matter go? Why, as units of matter, are we here? One possible explanation is that some agent in the early Universe acted to separate out the matter and anti-matter into different areas thus preventing interaction and annihilation. However, if that was the case, we would expect to observe entire galaxies made of anti-matter in the same way that we observe galaxies made of matter. No such anti-matter galaxies have ever been detected. Hence, we are driven to a disturbing conclusion that there must have been an asymmetry introduced in into particle creation that allows more matter than anti-matter to be created. To date, the physical cause of this asymmetry is not known and represents one of the biggest unknowns in our current cosmology. But how big is this asymmetry? How much excess of matter over anti-matter was there? Can it be true that all of the stars and galaxies and things in the Universe are the residue of a tiny asymmetry? Although we don't know it's origin, we can determine the amount of asymmetry through direct measurements. The ulimate source of each CMB photon was through particle annihilation. By measuring the number density of CMB photons compared to the number density of protons in the Universe we determine the photon-to-baryon ratio. The intensity of the CMB corresponds to a space density of roughly 400 photons per cubic centimeter. This number is approximately 1 billion times larger than the number density of protons. Thus, the number of photons in the Universe greatly exceeds the number of matter particles. More specifically, this measurement indicates that for everyone billion anti-quarks that existed in the early Universe, there was 1 billion and one quarks. This small asymmetry is the matter residue that survived the early Universe to produce all the stars, galaxies and observers today. But again, what produced this asymmetry and why is it roughly one billion to one, instead of, say, one trillion to one, one million to one, etc, etc? Again, we don't know the physics that produced this exact asymmetry although there have been some suggestions that the particular form of the electro-weak symmetry breaking produced this particular value. This asymmetry, which was likely set up in the very early Universe also carries with it another possibility that is related to the physical nature of dark matter. Potentiall, particle creation at extremely early times could have created very massive particle pairs (millions of times more massive than a proton). In thermal equilibrium, these massive particles should have immediately combined with their anti-massive counter part and annihilated one another.However, there is a possibility that some small residue of very massive hadrons are left over. If so, they could be a major mass constituent in the Universe. These particles would be weakly interacting, meaning that they would not influence the dynamics of the early Universe or decay into smaller mass particles. Weakly interacting massive particles have been given the nickname WIMPS . If they really exist, there may be several of them whizzing through your body as you read this. To date, particle dark matter searches for WIMPS have not returned any strong evidence in favor of there existence. The Thermal History of the Universe Certain physical processes will occur in the Universe depending upon the temperature and density conditions at that time. Remember, both the temperature and density are rapidly falling as the Universe expands (ages). The universe will go through a particular series of stages that are dominated by a single physical process. Stage 1: The Universe at 1/100 of a Second: Proton-Neutron Equilibrium: By about 0.01 seconds, the temperatures and densities have rapidly fallen from their initial values. At this time, the univese has cooled to T = 100 billion degrees and the density has dropped down to about 1 billion grams per cubic centimeter. While these conditions are still more extreme than found in any star, the density now has dropped well below nuclear density so its now possible for individual atoms to exit.The constituents of the Universe at this time are: Protons, neutrons, electrons and neutrinos One billion photons for each proton, neutron, and electron matter and energy exist in thermal equilibrium Now we introduce another particle character, the neutrino. Neutrinos serve a very important role in particle interactions as they can serve as agents to change Protons into Neutrons and vice versa. Ordinarily, neutrinos do not easily interact with other forms of matter, however, in cases of high density, the neutrinos can not travel through the matter without interacting. At this time the Universe is still so dense that it is opaque to neutrinos. Opaque means that the neutrino can not travel through the Universe (at this time) without suffering an interaction. The opposite of opaque is transparent . If the Universe is said to be transparant to neutrinos that means that they can move through that Universe without interacting; the rest of the matter in the Universe essentially doesn't exist from the neutrino's point of view. But at this early time (0.01 seconds) neutrino's are strongly interacting via the following interactions: anti-neutrino+proton <----> neutron+anti-electron neutrino + neutron <------> proton + electron In these two reactions we can see that neutrinos are the mediating agent which allows protons to be converted to neutrons and vice-versa. These neutrino interactions keeps the number density of protons and the number density of neutrons constant. That is, there is thermal equilibrium between protons and neutrons. A a free neutron will decay in about 900 seconds (its half-life). At t = 0.01 seconds, none of the neutrons have decayed and furthermore, new neutrons are being made from protons. So, as long as the neutrinos can interact with neutrons and protons, this balance will be kept. Hence the proton-to-neutron ( p/n ) ratio is 1. Stage 2: The Universe at 1 Second old. The Neutrons Begin to Decay Away At this time the Universe has cooled to 10 billion degrees ((still hotter than centers of stars) and the density is around 1000 grams per cubic centimeter. Two important changes are now occurring: No more proton-anti-proton or neutron-anti-neutron pairs can be created from the radiation field. The average energy per photon is now too low so only light particles (like electrons) can still be produced via pair production. The Universe now becomes transparent to neutrinos and thus the neutrions are no longer interacting with the photons and the neutrons. Now, no new neutrons can be created by any mechanism. If the neutrons remains as free neutrons (and don't end up being bound into an atomic nucleus) then they simply decay away into oblivion. A Universe without neutrons will have no elements (heavier than hydrogen) in it and hence no planets, no life, no internet, very sad. Fortunately, the Universe will find a natural mechanism for preserving most of the neutrons. However, the neutrons are rapidly decaying and at about 1 second the ( p/n ) ratio is about 2 as equilbrium is no longer in place. Stage 3: The Universe from 1-10 seconds: The Last Hurrah for the Electrons When the Universe is 10 seconds old, it has cooled to the point where the average energy per photon is less than the rest mass energy of any known particle, hence no particles can be created. However, in this interval of 1-10 seconds, the Universe is already below the threshold energy for the creation of protons and neutrons. Only very light particles like electrons (which have a rest mass energy 2000 times less than that of a proton or neutron) can be created in this window. This leads to the important physical situation that the reaction electron+anti-electron --> photon+photon is now greatly favored over the reverse reaction photon+photon --> electron+anti-electron. In fact, it is this electron + anti-electron annihilation that produces most of the photons that we now observe in the CMB and which produces the observed photon-to-baryon ratio since there were 1 billion and 1 electrons for every 1 billion anti-electrons. By t = 10 seconds the ( p/n ) ratio is now 3:1. No more particle creation is occurring from the photon field. The Universe consists of protons, neutrons and electrons plus a billion photons for each matter particle and non-interacting neutrinos. Stage 4: 10 seconds -- 3 Minutes The Dull domain of the Photons At the start of this epoch, the temperature of the Universe has cooled to 3 billion degrees and the density has dropped to 100 grams per cubic centimeter. No more particle creation is occurring and the abundance of electrons and anti-electrons now is constant. Remember, these are the lightest particles that we know of and hence have the longest formation window. All these electron and anti-electron pairs now annihilate thus producing the final photon background with the characteristic that there are one billion photons for each particle. During this epoch, however, stable atomic nuclei (e.g. Helium) can't form yet because the Universe is expanding very fast and is still filled with very high energy photons. These photons have energies higher than the binding energy of deuterium which is the necessary first step in the formation of Helium. As soon as a deuterium nucleus (which consists of a proton and a neutron forms), that nucleus would be immediately photo-dissociated. Remember, the Universe is still very small at this point and there are 1 billion high energy photons swarming about the protons and neutrons, so particles are constantly interacting with the photons. Without the ability to form Helium, the neutrons continue to decay and p/n continues to rise. At the end of this epoch p/n is 7 and the neutrons are starting to decay away completely. Stage 5: 3-20 minutes: The Onset of Helium Formation The Universe has now cooled to a temperature of a few hundred million degrees. The density is approximately 10 grams per cubic centimeter. The conditions of the Universe (temperature and density) are now very similar to the conditions inside a star. However, since the Universe is still expanding rapidly, the Universe is not like a star in the sense of being a stable place where the temperature and density remain constant. At this time p/n is 7 and the first steps of the proton-proton cycle begin. This is exactly the same thermonuclear fusion cycle that the Sun uses to generate its energy. The first step in the cycle is the fusing of two protons to make deuterium. Deuterium is an element with two nucleons, a proton and a neutron. It is hydrogen with an extra neutron in its nucleus and therefore is an isotope of hydrogen. We will refer to deuterium with the symbol 2H indicating that its hydrogen with 2 nucleons ( 1H is just a proton). In symbolic form, the reaction is H + H ==> 2H + positron + neutrino However, deuterium is a very fragile nucleus and can easily be broken apart by a high energy photon: 2H + photon ==> p + n and the neutron created in this way will decay unless it can bind with another proton to form an atomic nucleus. This competition between the creation of 2H via fusion and its destruction via photo-dissociation sets up an interesting race condition. Will deuterium combine with another proton to make a nucleus with 3 nucleons or will it be photo-dissociated before it can do this? This race condition depends on the density of protons: if the density is high then deuterium will fuse with another proton to make 3He if the density is low then most of the deuterium will be photo-dissociated before making 3He a high density Universe means a low density of deuterium a low density Universe means a low density of helium because most of the deuterium is destroyed before it can be fused into helium. Because of this, if we can measure the deuterium and helium abundances in the Universe, we can get a handle on what the proton density was initially. Measuring the helium abundance is significantly easier than measuring the deuterium abundance and so we have the most observational data for that. The next step in the proton-proton chain is 2H + H ==> 3He + photon 3He is a new element that has two protons in its nucleus. Each element in the periodic table has a unique number of protons in its nucleus. Isotopes of those elements are formed whenever there are different numbers of neutrons (could be more, could be less) in the nucleus. The most common form of helium is 4He: 2 protons + 2 neutrons. Helium with only one neutron in its nucleus is still helium (because there are 2 protons). So 3He is an isotope of helium. Once 3He is formed, the next step of the reaction can occur fairly quickly because 3He has a relatively high binding energy and is not susceptible to photo-dissociation. The final step in the proton-proton chain is 3He + 3He ==> 4He + p + p where we now have formed stable 4He. If it were not for the formation of 4He, then the Universe would be devoid of neutrons. Thus the free neutrons created in the early Universe end up in 4He nuclei. The Predicted Helium Abundance Prior to the epoch of nucleosynthesis, the p/n ratio was 7. So for every 14 protons there are 2 neutrons. The end result of the proton-proton changes is the conversion of 2 protons and 2 neutrons into 1 4He nucleus. Hence, after the reaction our initial mix of 14 protons and 2 neutrons has been changed to 12 protons and 1 4He nucleus. The mass of 4He is approximately 4 times the mass of a proton. This leads to a very specific prediction for the mass fraction of the Universe which is in the form of helium: where the masses in the above equation are all in units of proton mass. The prediction that the helium mass fraction is 25% has been confirmed many times via observation. If this were not the case, we would have a severe blow to our model. The good agreement between the prediction and the actual observations provides further support of the Hot Big Bang model. Overall, the abundance of helium is sensitive to three parameters: The p/n ratio at the time that nucleosynthesis starts The ratio of photons to baryons The actual baryon density The good agreement between theory and observation suggests that our estimate of these quantities can't be too far wrong. Elements beyond Helium In addition to making 4He , there is some limited nucleosynthesis that acts to build heavier elements. These reactions are 3He + 4He ==> 7Be + photon 7Be + electron ==> 7Li + photon 7Li + proton ==> 7Li + neutrino 7Be + proton ==> 8Bo + photon 8Bo ==> 8Be + anti-electron + neutrino 8Be ==> 4He + 4He In the above reaction sequences one can see that the usual end product is a return to 4He. However, these reactions don't necessarily go to completion (because the Universe is expanding) and so trace amounts of 7Li (Lithium) should also exist. Observations have tried to detect these trace amounts in the oldest stars in our Galaxy with some limited success. The observed abundances agree well with the predictions of Big Bang nucleosynthesis. However, this element production stops at 8Bo (Boron) which has 5 protons and 3 neutrons in its nucleus. Heavier elements cannot be produced because: 8Bo is very unstable (1/2 life = 0.8 seconds) and rapidly decays into the even more unstable element 8Be (1/2 life ~ 10-17 seconds) which rapidly decays back into two 4He nuclei. This short half life makes it impossible for either Boron or Beryllium to capture a 4He to make Carbon. The Universe is cooling too fast for the triple-alpha reaction to occur. Namely 4He + 4He + 4He ==> 12C does not occur. We are now done with element production. At this point the Universe consists of photons and the elements H,2H,3He,4He,7Li as well as one billion photons per hydrogen atom. At this time these photons all have energies sufficient to ionize hydrogen and helium. Thus, in addition to a sea of photons, a sea of free electrons also exists and this has a very important physical effect. The Epoch of Decoupling When the Universe is 20 minutes old, the temperature has now decreased to 1 million degrees and thermonuclear fusion stops. However, the energy per photon is still very high so that no neutral atoms exist. That is, the average energy per photon is still much higher than the ionization energy of either Helium or Hydrogen and so all of the electrons are free, and not bound up in neutral atoms. This network of free electrons serves as a scattering network for the photon as photons interact with electrons are scattered. An electron-photon scattering event does not change the energy of the photon, but merely its direction. So, at this time, photons can not free stream (move in astraight line)as their direction of motion will get randomly changed with each electron scatterin event as shown below: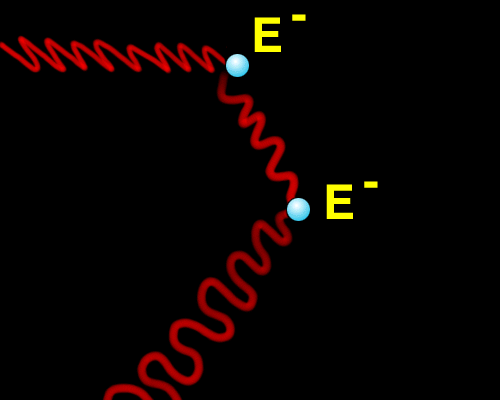 A photon wavy red line above that encounters a free electron will have an interaction with the electron because it has an electric field. This interaction takes the form of scattering. thus altering the direction of motion of the photom Now since the photons are being scattered constantly in random directions by the free electrons, the photons themselves have no net direction and therefore they can never leave the free electron network. In this way, the electron-scattering mechanism keeps the photons coupled to the matter. Under this conditions, the Universe is opaque to photons. Each individual photon will experience multiple scatterings by this network of free electrons. There is essentially no way the photons can escape from this network; they are constrained to "bounce" around inside of it but never escape from it. The following analogy/animation may make these points clearer: Roo Animation goes here Suppose that you are in your astronomy lecture room on campus. You are also scheduled to meet your friend outside of the lecture room, for sanity maintenance after yet another pointless astronomy lecture. In this case, you represent the signal and the outside of that room represents the Universe where your friend, the observer is waiting. The lecture room has no windows so there is no way that your friend (hereafter the observer) can directly detect you inside the sealed room. You have to physically exit the door for your signal to be observed in the Universe. Now suppose you are the only student in that room because your the only survivor of the pointless lecture torture. Obviously in this case, when the latest torture is over, you simply bolt from your seat to the door, exit the door, and voila, become existent in the observable Universe. However, one day you show up for lecture and the professor brings in a surprise. All of a sudden you are surrounded by a network of kangaroos with boxing gloves jumping up and down and flailing their arms. The density of roos, in fact, is so high that you can no longer actually see the professor, but you can still hear them. Now, when the pointless boring lecture ends again, as you try to make your way out of the room, you encounter one of these renegade roos who punches you in a benign manner but which randomly alters your direction of motion, until you encounter another roo who again randomly alters your direction or motion. Assuming you can survive the renegade roo punches, you should realize that you are not getting out of this room anytime soon. So the oberver now has to wait a longer time for your signal because your direction of motion is no longer free streaming. Thus, you are opaque with respect to the network of roos. Only when the roo density drops can you exit the room and "stream" out into the Universe. The existence of the scattering network delays your signal to all external observers. The tight coupling between the radiation and matter means that the matter should be distributed like the radiation and we know, from observations of the CMB, that the distribution of radiation is very smooth. If the matter distribution were to become completely smooth, then there would be no collapse into individual clumps which could grow into galaxies eventually. We will examine this dilemma more in Chapter 5 because it is somewhat challenging to understand and likely requires the presence of some kind of matter that is immune to the effects of radiation pressure in the early universe. Since the free electron network is the coupling mechanism then as long as the universe remains ionized, the matter and radiation (photons) can never decouple. Recall that in Chapter 2 we showed that the energy density in the radiation field naturally decreases much faster than the energy density in the matter field. Eventually this means the Universe will cool to the point where the electrons can recombine with the protons. When this happens, the scattering network of free electrons is now gone and the radiation has no mechanism to couple to the matter. Thus, there is some surface of last scattering in the evolution of the Universe from which the photons are finally no longer scattered but free stream to fill the Universe. This creates the CMB signal that we observe. The observed signal is greatly redshifted from the time of its creation when the temperature was approximately 3000 K (see below). Prior to this time, no external observer (e.g. us) could get any signal because the photons were still being scattered around. Perhaps the following thought experiment can help to better understand the relation between the surface of last scattering and information received by detectors. Suppose you go to a baseball game and sit in the center field bleachers. Under most circumstances you have a clear view of the pitcher and the batter. The pitcher throws a pitch to the batter who hits a home run right at you. What do you observe? You observe the source of the baseball that you are about to catch as being the bat swung by the hitter. Nothing has interfered with the production of the home run and its trajectory to you. Now, imagine that the baseball field is filled with a network of indestructible windmills. When a hit baseball strikes a windmill, the direction of the baseball's motion will be randomly altered (we assume the baseball is also indestructible). The scattering network is so thick that you can't see the pitcher or the batter. In fact, you will never even see the baseball until it emerges from the last row of the windmills because only then can the baseball be scattered towards the bleachers. Hence, the last row of the windmills is the last scattering surface and the observer only sees baseballs (photons) emerging from this source. Of interest to understanding the overall evolution of the Universe is the actual time it takes for the electrons to recombine with the protons so that radiation and matter become decoupled. This depends on two things: 1. The ionization energy of hydrogen ( 13.6 electron volts (eV) ) 2. The ratio of photons to protons Figure Distribution of photon energies for a temperature of 3000 K. The point marked A represents the average energy per photon. The point marked 13.6 represents the ionization energy of hydrogen. All photons with energies greater than this will ionize hydrogen. Photon energy is increasing to the left in this curve. Even though only a small percentage of the total number of photons is contained in the region of the curve above 13.6 eV, the large ratio of photons to protons means that the matter can still be ionized at this temperature. For the conditions of our Universe, this time is approximately 100,000 years and we can understand this timescale as follows: Normally, a temperature of 50,000 K is required to ionize hydrogen (e.g. like an H II region in our galaxy). At this temperature, the average energy per photon corresponds to the ionization energy of hydrogen. However, in the early Universe, there are many more photons than protons so even at lower temperatures, there will be still enough ionizing photons to continue the ionization. This is why the timescale depends on the ratio of photons to protons. If that ratio were larger, the timescale would be longer and the tendency to produce a smoother mass distribution would be larger. In fact, no galaxies might have even formed if the ratio of photons to protons was significantly higher than 1 billion to one. As schematically shown in Figure 3.7, the number of ionizing photons will become less than the number of hydrogen atoms when the Universe has cooled to 3000K. This means that an electron can recombine with a proton without fear of being immediately re-ionized because the number of ionized photons is lower than the number of electron-proton pairs. Recombination therefore occurs at a temperature of 3000 degrees. The photons now no longer interact with the matter and free stream to fill the Universe. This is what we presently observe as the 3 K microwave background. This radiation has been redshifted by a factor of 1000 by the time the Universe has aged to 10 billion years and we detect it. This also means that we cannot observe the Universe when it was younger than 100,000 years in the same way that you cannot observe a baseball from the bleachers until it has reached the surface of last scattering, even though the baseball was "created" at a much earlier time. After recombination has occurred, radiation is no longer an influence on the distribution of matter. Hence, matter will clump around any surviving density enhancements. The question now becomes, how did those density enhancements survive the radiation dominated era, and what is their nature? Ultimately these density enhancements have to grow to produce the structure we observe today. Since photons can be temporarily trapped in these structures and either gain or lose energy as they traverse them, their signature is imprinted on the CMB. We are now done with the radiation dominated history of the Universe and the next two chapters will move on the matter dominated era. There we will focus on 1) observations that help us determine the overall size scale and mass density of the Universe 2) observations that suggest the presence of large amounts of dark matter and, 3) how structure actually formed in the Universe. Summary (this figure needs to be redone) Time line of the early Universe with important events noted. This chapter has detailed the evolution in the first few seconds and minutes of the Universe. The evolution is characterized by rapid expansion and cooling. Different physical regimes can be defined depending upon the temperature and density of the Universe. Important events that occurred in this evolution are graphically represented in Figure 3.8. The first second of the Universe is characterized by the conversion of mass into energy and vice versa. The reaction rate is so large that conditions of thermal equilibrium exist. That is, the behavior of the Universe at any epoch is dependent on its temperature and not what happened prior to that time. Temperature. At early times, the energy density of the photons was so high that you could get particle creation from the photon field and/or energy creation from the matter field. photon+photon <=====> particle + anti-particle The kinds of particles +anti-particles that are created depends strictly on the average energy per photon which depends only on the temperature. If the photon energy is less than mpc2 then mp can't be created. Only particles with mass less than mp will be created. ( mp just represents the rest mass of some generic particle). Since a proton is 2000 times heavier than an electron, the window of opportunity for creating electrons/anti-electron pairs from the photon field is a lot longer than for creating protons/anti-proton pairs. In the early Universe the following regimes can be defined: In the very early Universe (prior to 10-11 seconds), lots of strange pairs of hadronic particles could have been produced from Quantum Fluctuations. We know very little of the physics that would be operative in this regime. From 10-6 seconds to 0.1 second was the window of opportunity for creating protons and neutrons and other "normal" particles. The Universe was opaque to neutrinos prior to it being a second old and this kept the abundance of protons equal to that of neutrons. At 1 second the neutrinos escape and the neutrons start to decay. The only thing that prevents their decay to zero is the formation of atomic nuclei via thermonuclear fusion. This fusion epoch starts around t=3 minutes and lasts until t=15 minutes. The proton-to-neutron ratio at the start of this epoch is 7-to-1. This ratio makes a solid prediction that the Helium Abundance of the Universe should be approximately 25%. This value is observed. From 15 minutes to approximately 100,000 years the Universe was radiation dominated. This means that gravity was not effective in trying to clump together ordinary baryonic matter as the radiation pressure would try to smooth out any clumps that could have formed. The existence of galaxies, therefore, may require some exotic form of matter in the Universe which was unaffected by this radiation pressure. From 15 minutes to approximately 100,000 years the Universe remains opaque to this radiation because the radiation and matter are coupled due to electron scattering. The radiation can only free itself from the matter when the Universe cools to the point where the free electrons can recombine with the protons and the Universe is no longer ionized. This occurs at a temperature of 3000 K and is the source of the CMB radiation that we now observe. The three big unknowns in the above sequence are: 1. What is the physics of the very early Universe when all the forces were unified? 2. What physics determined the masses of the particles? That is, why does a proton have the mass that it does? 3. What physics determined the matter-vs-anti-matter asymmetry?. That is, why for every 1 billion anti-protons were there 1 billion and 1 protons? Once the radiation dominated Universe has ended, structure can form and the Universe that we observe today can come into existence from fluctuations in the distribution of matter. How these fluctuations survive the radiation dominated era is currently a mystery.