After recombination there were obviously pockets of density enhancements around which material accumulated

The exact mechanism for this is unclear and most of the mass is probably darkmatter. Gravitational coalescence of this dark material then built the galaxies we observe today. Below is an N-body supercomputer simulation of this process. Note the evolution from many small clumps of matter to just a few large clumps.

• Galaxy Formation (?)

These eventually grow to form galaxies. Unfortunately, there is a rather wide range of different galaxy types, shapes and densities which means the formation process was not simple. Also most all galaxies today are embedded in some larger scale structure. The formation of these structures is unclear but here are a couple of possibilities:

• Large Scale Structure (a 22 Meg mpeg).
• Formation of a single Galaxy Cluster

Structure formation could have either occurred from fragmentation of very large regions into smaller regions or from the gravitational coalesence of sub-units into successively large structures. Both formation scenarios lead to a highly clustered Universe with structure on many different size scales.

However, no matter what form you are talking about, Dark Matter plays a central role as luminous matter will be drawn into the network of dark matter filaments.

The Dark Matter Universe

What is Dark Matter?

Objects which emit light, whether they are cigars, light bulbs, cows, stars or galaxies can be characterized by their emitted energy per unit mass. This is parameterized as the Mass to Luminosity ratio or M/L. For cosmological purposes, it is most convenient to express M/L in terms of solar masses and luminosities. For main sequence stars it can be shown that L is proportional to M^3.5-4 . Thus, a 10 solar mass star star has M/L of approximately 0.001, a 1 solar mass star has M/L =1 and a 0.1 solar mass star has M/L of approximately 1000. The term "dark matter" refers to the the existence of objects which have extreme M/L. Identifying the nature and extent of the dark matter component in the Universe is, arguably, the most significant unsolved problem in all of cosmology.

• Dark matter is material that gravitates but does not emit very much light.
• More specifically, it is material which has a high ratio of mass-to-luminosity

How do we know its there?

On scales of galaxies and clusters of galaxies, there is ample evidence for dark matter. This comes from the form of galaxy rotation curves. Figure 5.1 shows an image of a typical edge-on spiral galaxy, where the thin disk and central spherical light concentration are evident.

Figure 5.2 Schematic representation of the rotation curve of a galaxy. If most the mass of the galaxy is in the center, then one expects smaller rotational velocities with increasing distances from the center of the galaxy. This is shown in the dashed line and is not what is actually observed. Instead, rotation curves of the form depicted by the solid line are observed. The observation that the rotational velocity is constant after some radius implies that the mass of the galaxy must be in a greatly extended (relative to the light) distribution.

If the distribution of light traces the distribution of mass, then we would expect a high mass concentration that corresponds with the bulge light. In that case, the galaxy is similar to the point mass approximation that governs Solar System orbits in which the orbital velocity decreases with distance from the point mass. The expected rotation curve would then look like the dashed line shown in Figure 5.2. Observations, however, reveal a significantly different picture as most all galaxy rotation curves have a rotational velocity that rises slowly and then flattens out. This is shown as the solid line in Figure 5.2.

Figure 5.3 A rotation curve of a spiral galaxy. The center of the galaxy is at r = 0 and both halves of the galaxy rotation curve are shown here. The higher velocity side is rotating away from the observer and the lower velocity side would be rotating towards the observer. The galaxy quickly reaches its maximum rotational velocity at a relatively small radius and maintains that velocity out to the limits of the data.

In Figure 5.3 we show a typical rotation curve for a real spiral galaxy. These data show that the point mass approximation is invalid. The existence of flat rotation curves of galaxies can only be explained if the mass of the galaxy is increasing in direct proportion to the radius. We can understand this by referring to the derivation of Kepler's Third Law that was done in Chapter 1. Newton was able to show that for an object in circular orbit, the orbital velocity is determined by the total mass enclosed within the radius. In equation form, this is given by

M(r) ~ V² R

Flat rotation curves mean that V and hence V² is constant. The only way that can be achieved is if M(r)/R is a constant. Thus, the enclosed mass M(r) must continue to increase with increasing radius. However, since the light intensity is decreasing with increasing radius, this means that there must be substantial amounts of dark matter located at large radii in galaxies or, more specifically, that M/L must increase with increasing R.

Flat rotation curves can be reproduced in a model that assumes that most of the mass of the galaxy is distributed in a spherical halo around the disk. Since these halos contain very little light, they must be composed mostly of dark matter. Analysis of galaxy rotation curves suggests that approximately 90% of the mass of the galaxy is in the form of dark matter which is distributed in a spherical halo around the galaxy.

Mass of a galaxy grows with radius. Requires dark matter halo.

Clusters of Galaxies

Figure 5.5 A typical cluster of galaxies. The individual members do not escape from the cluster as sufficient mass exists to prevent the expansion of the cluster.

Clusters of galaxies represent a region of the Universe in which the mass density is sufficiently high that the expansion has been overcome. An example cluster is shown in Figure 5.5. This mass density serves to randomize the velocities of the cluster members as they assume some orbit in the cluster of galaxies. In that sense, galaxies in clusters are very much like the molecules inside a balloon of fixed volume. The galaxies can't escape and their overall relative velocities are determined by the mass of the cluster. The molecules in the balloon can't escape either and their overall velocity is determined by the temperature of the balloon. Thus, in a cluster of galaxies mass is analogous to temperature and indeed, this analogy explains why clusters of galaxies often emit X-rays. If the cluster is sufficiently massive it can heat the intracluster gas to high temperatures where it emits X-rays. This gives us an immediate diagnostic tool.

If we simply measure the relative velocities of the galaxies we can infer the total mass of the cluster. A small complication enters in that one needs to know the exact shape of the cluster; a spherical cluster is different than one that is shaped like a pancake - but the general principal applies. That dynamical mass estimate can then be compared to the mass estimate based on counting the number of galaxies in the cluster and adding up all their light. When this is done, it is typically found that the luminous galaxies in the clusters can only provide 5-10% of the total mass required for the cluster to exist. Taking into account the mass provided by the hot intracluster gas only raises this contribution by about a factor of 2.

Figure 5.6 The cluster Abell 2218. The appearance of "arcs" in the image is a manifestation of the distortion of the images of background galaxies by the lensing mass of the cluster.

Another means of estimating the mass of a cluster again appeals to gravitational lensing. In this case, it is the entire mass of a cluster that acts collectively as a lens. Figure 5.6 shows a spectacular example of this phenomena. Here, numerous arc-lets and rings can be seen. These are the distorted (lensed) images of resolved galaxies located behind the cluster. The orientation and degree of curvature of these features depends upon the cluster mass distribution and the overall amount of mass. Again, when the mass is inferred in this manner and compared to the luminous galaxies in the cluster, a substantial mass discrepancy exists. When this evidence is combined with the velocity data, there is little doubt that in clusters of galaxies, a substantial amount of dark matter must be present.

Gravitational Lenses

A Regular Lens:

A Galaxy can be a Lens:

Curved spacetime is the Lens:

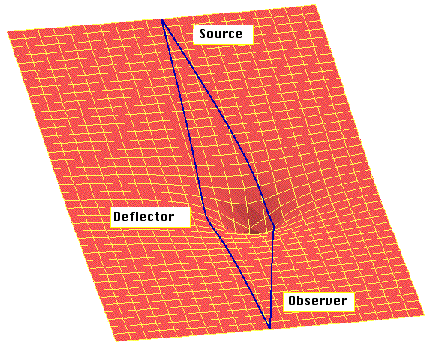
Different shapes can be seen as the orientation between the observer and the distant galaxy changes

Courtesy of Ned Wright, UCLA

So the evidence for Dark Matter is fairly overwhelming. Well how much of it is there and what is it?

• Theory: if the Universe is closed then all the luminous matter seen in galaxies contributes only 0.5% of the mass required to eventually halt the expansion

• Best argument: baryonic density fluctuations will not produce galaxies you need a heavy particle that is not effected by radiation pressure in order to eventually form galaxies

• This means that galaxies are surrounded by dark matter halos which trapped baryonic gas (e.g. hydrogen) and turned it into stars. So a galaxy like this is surrounded by an invisible dark matter halo.

What are the candidates

Baryonic: (e.g. made of protons and neutrons)

• Beer cans
• Jupiter size objects
• very low mass stars
• black holes and other stellar remnants

Non-baryonic (exotic matter):

• neutrinos with mass ratio of MWB photons to neutrinos is 4 to 1 therefore even a tiny neutrino mass has cosmological significance
• WIMPS - weakly interacting massive particles created in the extremely early universe
• Particles associated with symmetry breaking

How much dark matter is there?

• Theory 99% of the Universe is Dark Matter
• Observations 90% of the Universe is Dark Matter and the Universe is open

  There is a big difference between Theory and Observation with good arguments coming from both sides. The situation is unresolved and has been for 20 years. Whomever solves the "dark matter" problem will likely win the Nobel prize.

  However, its important to realize that the "dark matter" problem exists only in the context of one known long range force (gravity). Suppose there is another long range force that we are ignorant of. If this is discovered by future physicists then they will look back at this "dark matter" cosmology much the same way we now view the early "geocentric" cosmologies.