The Epoch of Decoupling
When the Universe is 15 minutes old, the temperature has now decreased
to 1 million degrees and thermonuclear fusion stops. However,
the energy per photon is still very high so that no neutral atoms
exist. The Universe is completely ionized at this point.
It is an expanding sea of mostly photons in which
are mixed small amounts of atomic nuclei and free
electrons. There is a physical mechanism, called
electron scattering, which now couples the distributions of matter
and radiation, rendering the Universe opaque to its own radiation. This
method works as follows (see Figure 3.4).
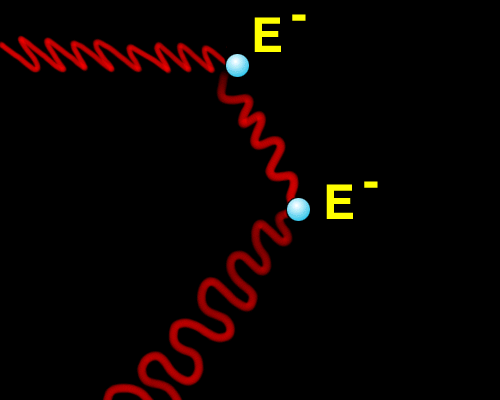
Figure 3.4 Visualization of photons
(gray wavy lines) having their direction of motion changed when
they encounter an electron. This is electron scattering.
|
A photon that encounters a free electron will have an interaction
with the electron because it has an electric field. This interaction
takes the form of scattering. Scattering randomly alters the
direction of motion of the photon in the same way that the renegade
Kangaroos randomly altered the motion of the student discussed earlier.
There is no photon energy loss in this process, the photon merely
changes its direction of motion until it encounters another free
electron and is scattered again. So each individual photon will
experience multiple scatterings by this network of free electrons.
There is essentially no way the photons can escape from this network;
they are constrained to bounce around inside of it. The only way
to escape is when the free electrons disappear and become bound to
atomic nuclei. This will only occur when the Universe cools to the
point that it is no longer ionized. For the moment, we have
1 billion ionizing photons per electron and so every time this
reaction tries to occur:
proton + electron ==> H-atom
it is immediately undone by this reaction
H-atom + photon ==> proton + electron
The matter and radiation are in thermal equilibrium
so the matter temperature is also a million degrees and therefore
it will not easily clump. Moreover, there is momentum transfer
or radiation drag produced on the matter by the radiation
field so every time two matter particles try to get together, the
process is interrupted by the radiation field. This is schematically
shown in Figure 3.5. This leads to a big problem. How is the
Universe ever going to grow a galaxy if matter can not clump
together to start the process?
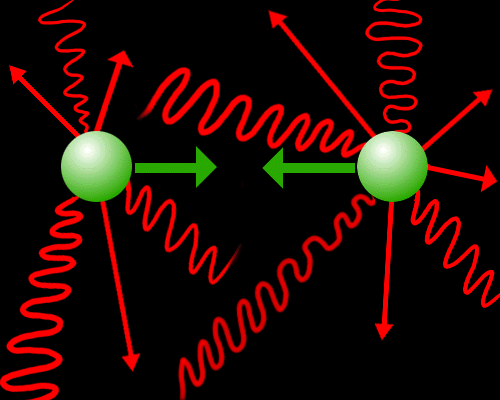
Figure 3.5 Visualization of two
mass particles being bombarded by radiation and
thus unable to gravitational "stick" together. The red arrows
indicate the random directions of momentum the particles
get when they are struck by the radiation. The arrows
represent gravitational attraction.
|
The tight coupling between the radiation and matter means
that the matter should be distributed like the radiation and we
know, from observations of the CMB, that the distribution of
radiation is very smooth. If the matter distribution were to
become completely smooth, then there would be no collapse into
individual clumps which could grow into galaxies eventually.
The coupling between matter and radiation will continue as
long as the Universe remains ionized. Recall that earlier
we showed that the energy density in the radiation field naturally
decreases much faster than the energy density in the matter field.
Eventually this means the Universe will cool to the point where the electrons can
recombine with the protons. When this happens, the scattering
network of free electrons is now gone and the radiation has no
mechanism to couple to the matter.
Thus, there is some surface of last scattering in the evolution
of the Universe from which the photons are finally no longer
scattered but free stream to fill the Universe. This creates the
CMB signal that we observe. The observed signal is greatly redshifted
from the time of its creation when the temperature was approximately
3000 K (see below). Prior to this time, no external observer
(e.g. us) could get any signal because the photons were still
being scattered around. Perhaps the following thought experiment
can help to better understand the relation between the surface of last
scattering and information received by detectors.
Suppose you go to a baseball game and sit in the center field
bleachers. Under most circumstances you have a clear view of the
pitcher and the batter. The pitcher throws a pitch to the batter
who hits a home run right at you. What do you observe? You
observe the source of the baseball that you are about to catch
as being the bat swung by the hitter. Nothing has interfered with
the production of the home run and its trajectory to you. Now,
imagine that the baseball field is filled with a network of
indestructible windmills. When a hit baseball strikes a windmill,
the direction of the baseball's motion will be randomly altered
(we assume the baseball is also indestructible). The scattering
network is so thick that you can't see the pitcher or the batter.
In fact, you will never even see the baseball until it emerges from
the last row of the windmills because only then can the baseball
be scattered towards the bleachers. Hence, the last row of the
windmills is the last scattering surface and the observer only
sees baseballs (photons) emerging from this source.

Figure 3.6 Visualization of scattering.
See text for a description.
|
This concept of scattering is shown as an artist conception in
Figure 3.6. Here we see a detector (the eyeballs on the horizon)
with some photons (blue and red balls) heading towards it. Imagine
the source of the photons has a cannon shooting balls. Between
the cannon and the detector is a scattering network (windmills
in this case). As the photons enter into the scattering network
their direction of motion changes and few of them will actually
reach the detector. If the scattering network is sufficiently
thick, then you can not see the source of the photons (the cannon)
but would only observe photons coming out in random places out
of the network. If you image the space outside the network as
the Universe, then its easy to see that scattering will produce
a homogeneous distribution of photons. If we shoot enough cannon
balls into the scattering network, a ball will be scattered to
every point in the "Universe".
Of interest to understanding the overall evolution of the Universe is
the actual time it takes for the electrons to recombine with
the protons so that radiation and matter become decoupled. This
depends on two things:
1. The ionization energy of hydrogen ( 13.6 electron volts (eV) )
2. The ratio of photons to protons

Figure 3.7 Distribution of photon energies
for a temperature of 3000 K. The point marked A represents the
average energy per photon. The point marked 13.6 represents the
ionization energy of hydrogen. All photons with energies greater
than this will ionize hydrogen. Photon energy is increasing to
the left in this curve. Even though only a small percentage of
the total number of photons is contained in the region of the curve
above 13.6 eV, the large ratio of photons to protons means that the
matter can still be ionized at this temperature.
|
For the conditions of our Universe, this time is approximately
100,000 years and we can understand this timescale as follows:
Normally, a temperature of 50,000 K is required to ionize
hydrogen (e.g. like an H II region in our galaxy). At this temperature,
the average energy per photon corresponds to the ionization energy
of hydrogen. However, in the early Universe, there are many more
photons than protons so even at lower temperatures, there will be
still enough ionizing photons to continue the ionization. This
is why the timescale depends on the ratio of photons to protons.
If that ratio were larger, the timescale would be longer and the
tendency to produce a smoother mass distribution would be larger.
In fact, no galaxies might have even formed if the ratio of
photons to protons was significantly higher than 1 billion to one.
As schematically shown in Figure 3.7, the number of ionizing photons
will become less than the number of hydrogen atoms when the Universe has
cooled to 3000K. This means that an electron can recombine with
a proton without fear of being immediately re-ionized because the
number of ionized photons is lower than the number of electron-proton
pairs.
Recombination therefore occurs at a temperature of 3000 degrees.
The photons now no longer interact with the matter and free stream
to fill the Universe. This is what we presently observe as the
3 K microwave background. This radiation has
been redshifted by a factor of 1000 by the time the Universe
has aged to 10 billion years and we detect it.
This also means that we cannot observe the Universe when it
was younger than 100,000 years in the same way that you cannot
observe a baseball from the bleachers until it has reached the
surface of last scattering, even though the baseball was
"created" at a much earlier time.
After recombination has occurred, radiation is no longer an
influence on the distribution of matter. Hence, matter will
clump around any surviving density enhancements. The
question now becomes, how did those density enhancements
survive the radiation dominated era, and what is their nature?
Ultimately these density enhancements have to grow to
produce the structure we observe today. Since photons can be
temporarily trapped in these structures and either gain or
lose energy as they traverse them, their signature is
imprinted on the CMB. This density fluctuation signature is what COBE detected in
the form of temperature fluctuations (see Figure 2.8).
We are now done with the radiation dominated history of the Universe
and the next two chapters will move on the matter dominated era.
There we will focus on 1) observations that help us determine the
overall size scale and mass density of the Universe 2) observations
that suggest the presence of large amounts of dark matter and, 3)
how structure actually formed in the Universe.
Summary

Figure 3.8 Time line of the
early Universe with important events noted.
|
This chapter has detailed the evolution in the first few seconds
and minutes of the Universe. The evolution is characterized by
rapid expansion and cooling. Different physical regimes can be defined
depending upon the temperature and density of the Universe. Important
events that occurred in this evolution are graphically represented
in Figure 3.8. The
first second of the Universe is characterized by the conversion of
mass into energy and vice versa. The reaction rate is so large that
conditions of thermal equilibrium exist. That is, the behavior
of the Universe at any epoch is dependent on its temperature and
not what happened prior to that time.
Temperature.
At early times, the energy density of the photons was so high
that you could get particle creation from the photon field
and/or energy creation from the matter field.
photon+photon <=====> particle + anti-particle
The kinds of particles +anti-particles that are created depends
strictly on the average energy per photon which depends only
on the temperature.
If the photon energy is less than mpc2
then mp can't be created.
Only particles with mass less than mp
will be created.
( mp
just represents the rest mass of some generic particle).
Since a proton is 2000 times heavier than an electron, the
window of opportunity for creating electrons/anti-electron pairs
from the photon field is a lot longer than for creating protons/anti-proton
pairs.
In the early Universe the following regimes can be defined:
In the very early Universe (prior to 10-11
seconds), lots of strange pairs of hadronic particles
could have been produced from Quantum Fluctuations. We know very
little of the physics that would be operative in this regime.
From 10-6 seconds to 0.1 second was the window of opportunity
for creating protons and neutrons and other "normal"
particles.
The Universe was opaque to neutrinos prior to it being a
second old and this kept the abundance of protons equal to
that of neutrons.
At 1 second the neutrinos escape and the neutrons start to
decay. The only thing that prevents their decay to zero is the
formation of atomic nuclei via thermonuclear fusion. This
fusion epoch starts around t=3 minutes and lasts until t=15
minutes. The proton-to-neutron ratio at the start of this
epoch is 7-to-1. This ratio makes a solid prediction that
the Helium Abundance of the Universe should be approximately
25%. This value is observed.
From 15 minutes to approximately 100,000 years the Universe
was radiation dominated. This means that gravity was not effective
in trying to clump together ordinary baryonic matter as the radiation
pressure would try to smooth out any clumps that could have formed.
The existence of galaxies, therefore, may require some exotic form
of matter in the Universe which was unaffected by this radiation pressure.
From 15 minutes to approximately 100,000 years the Universe
remains opaque to this radiation because the radiation and matter
are coupled due to electron scattering. The radiation can only free
itself from the matter when the Universe cools to the point where the
free electrons can recombine with the protons and the Universe is
no longer ionized. This occurs at a temperature of 3000 K and is
the source of the CMB radiation that we now observe.
The three big unknowns in the above sequence are:
1. What is the physics of the very early Universe when all the
forces were unified?
2. What physics determined the masses of the particles? That
is, why does a proton have the mass that it does?
3. What physics determined the matter-vs-anti-matter
asymmetry?. That is, why for every 1 billion anti-protons
were there 1 billion and 1 protons?
Once the radiation dominated Universe has ended, structure can form
and the Universe that we observe today can come into existence from
fluctuations in the distribution of matter. How these fluctuations
survive the radiation dominated era is currently a mystery.
|




