Recall when we discussed the idea of quantum computing and the definition of a qubit, as a superposition of states in say a two bit system (e.g. spin up/spin down for a particle), that the qubit could never really be observed by the outside world because one of the states would disappear (remember the observed coin or the observec cat).

Well the idea of quantum entanglement may help here.



In the example below, a blue photon from the incoming light source undergoes 'down-conversion' inside a crystal (which heats up slightly) to form two lower-energy red photons. As these two red photons emerge from the crystal they are entangled - that is the measured polarization (state) of one uniquely determines the polarization (state) of the other.

In step 2 the energy of the entangled photons is converted to electron vibrations in some material (i.e. the metal film - physicists call these vibrations surface plasmons).

In step 3 the surface plasmons, which are very short lived, are inherently coupled to the original radiation field which causes the photons to be re-emitted, still in their entangled state.

In step 4 Polarizers placed in the path of these photons are set so that they pass only one particular form of polarization.

In step 5 they reach the detector. Why is this relevant?

This experiment shows that quantum entanglement can withstand various conversion processes. This raises the possibility that through the manipulation of surface plasmons (e.g. electronic vibrations in a material) one can control entangled photons, and thus control how information is generated in this system in principle, this is similar to the function of a transistor.

Another example of entanglement:

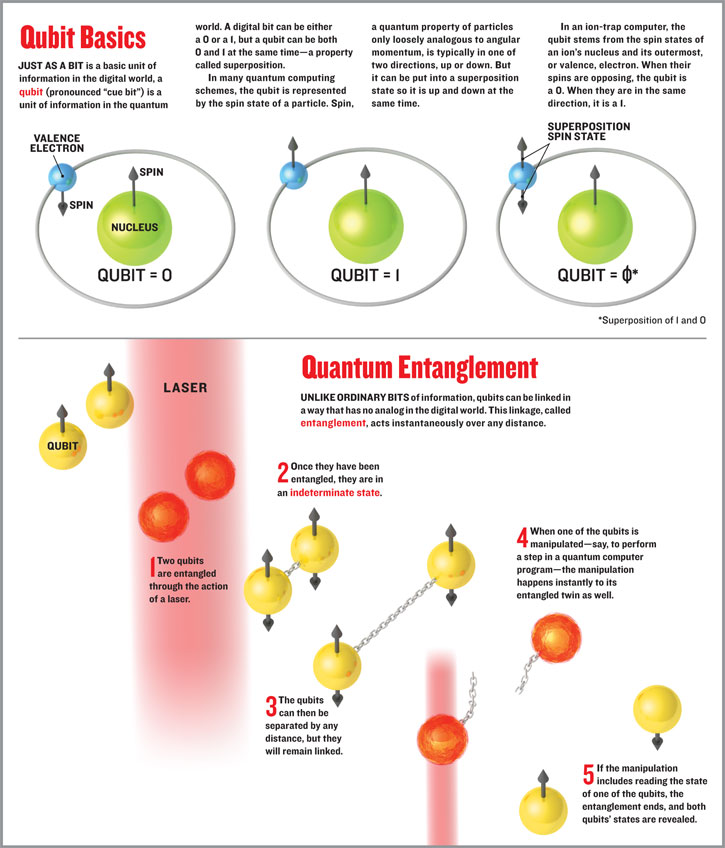
Suppose that we have two spin 1/2 particles ( think of them as coins that have a "heads" side that can be either up or down). They are in an entangled state such that 50% of the time particle A is found to be spin up (heads up) and particle B is spin down (heads down, i.e. tails), and the other 50% of the time A is found to be spin down and B is spin up.

Now, the important point about this entanglement is that it can never happen that A and B are found with both spins up or both spins down, so if we measure A and find that it is spin up, then we already know that B MUST be spin down, even before we measure it.

Now the amazing thing, in principle, is that A and B can be separated by a large distance.

Does this mean we just sent information faster than the speed of light?

NO: We only know what state B is in because we already knew the quantum state of the system made up of A and B at the beginning and we know the outcome of the measurement on A. The true test of whether information is sent is whether we're able to use this to send some sort of message to someone who is measuring particle B.

Ok, so let's say that George has particle A here on earth, and Dick is light years away in deep space (where he should be) with particle B.

They want to use their entangled pair to send a signal.

Well, if George measures A, he can't control which outcome he gets, so he can't control which outcome Dick gets. That is George can not impose a pre-determined outcome for the measurement of A.

That makes it hard to send any message.

Well, what if George and Dick have agreed that at noon George will measure A if he wants Dick to go pheasant hunting but won't measure A if he doesn't want him to go hunting.

So instead of using the outcome of the measurement to carry a message, George would send a message based on whether or not he measured the state (this is actually pretty clever on the part of George and Dick)

However, like most things that George and Dick do, this doesn't work either.

Reason: When George measures, 50% of the time he gets up and 50% of the time he gets down. That means that when Dick measures particle B after George has measured particle A, 50% of the time he will get down (corresponding to George's up) and 50% of the time he will get up(corresponding to George's down). The problem is that those are the same probabilities as in the case that George hasn't measured at all. So it seems this scheme just isn't going to work.

So yes, while something changed "faster than the speed of light" ( physicists call this the wave function), that change has no material consequence in terms of the propogation of a real information signal.

That is, the change in state only becomes directly observable when the two measurements are actually compared and that requires information transmission which can only be done at speeds less than or equal to light.

The big challange in quantum computing is then finding a way to make this wave function have a physical reality. To some of us, this seems impossible.