Galileo &
Galileo made extensive contributions to our understanding of the laws governing the motion of objects. The famous Leaning Tower of Pisa experiment may be apocryphal. It is likely that Galileo himself did not drop two objects of very different weight from the tower to prove that (contrary to popular expectations) they would hit the ground at the same time. However, it is certain that Galileo understood the principle involved, and probably did similar experiments. The realization that, as we would say in modern terms, the acceleration due to gravity is independent of the weight of an object was important to the formulation of a theory of gravitation by Newton.
Galileo also did experiments on projectile motion to clearly show just how wrong the Arisotelian concepts were:
Most objects in a state of motion do NOT remain in that state of motion. For example, a block of wood pushed at constant speed across a table quickly comes to rest when we stop pushing. Thus, Aristotle held that objects at rest remained at rest unless a force acted on them, but that objects in motion did not remain in motion unless a force acted constantly on them. Galileo, by virtue of a series of experiments (many with objects sliding down inclined planes), realized that the analysis of Aristotle was incorrect because it failed to account properly for a hidden force: the frictional force between the surface and the object.
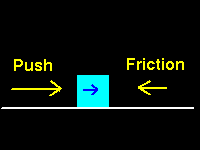Thus, as we push the block of wood across the table, there are
two opposing forces that act: the force associated with the push,
and a force that is
associated with the friction and that acts in the opposite direction.
Galileo realized that as the frictional forces were decreased (for
example, by placing oil on the table) the object would move further and further
before stopping. From this he abstracted a basic form of
the law of inertia: if the
frictional forces could be reduced to exactly zero (not possible in a realistic
experiment, but it can be approximated to high precision)
an object pushed at constant speed
across a frictionless surface of infinite extent will continue at that speed
forever after we stop pushing, unless a new force acts on it at a later time.
Galileo The Physicist
understanding
that ratios can lead to physical understanding as long as a consistent
measurement is done.
The "breakthrough" that Galileo was able to provide was in his recognition of what aspects of motion (physics) were universal. This ultimately led to his idea of frames of reference.
Aristotle held that there are two kinds of motion for inanimate matter, natural and unnatural. Unnatural (or "violent") motion is when something is being pushed, and in this case the speed of motion is proportional to the force of the push. (This was probably deduced from watching ox-carts and boats.) Natural motion is when something is seeking its natural place in the universe, such as a stone falling, or fire rising. (We are only talking here about substances composed of earth, water, air and fire, the "natural circular motion" of the planets, composed of aither, is considered separately).For the natural motion of heavy objects falling to earth, Aristotle asserted that the speed of fall was proportional to the weight, and inversely proportional to the density of the medium the body was falling through. He did also mention that there was some acceleration, as the body approached more closely its own element, its weight increased and it speeded up. However, these remarks in Aristotle are very brief and vague, and certainly not quantitative. Actually, these views of Aristotle did not go unchallenged even in ancient Athens. Thirty years or so after Aristotle's death, Strato pointed out that a stone dropped from a greater height had a greater impact on the ground, suggesting that the stone picked up more speed as it fell from the greater height. |
Two New Sciences
Galileo set out his ideas about falling bodies, and about projectiles in general, in a book called "Two New Sciences". The two were the science of motion, which became the foundation-stone of physics, and the science of materials and construction, an important contribution to engineering.The ideas are presented in lively fashion as a dialogue involving three characters, Salviati, Sagredo and Simplicio. The official Church point of view, that is, Aristotelianism, is put forward by the character called Simplicio, and usually demolished by the others. Galileo's defense when accused of heresy in a similar book was that he was just setting out all points of view, but this is somewhat disingenuous---Simplicio is almost invariably portrayed as simpleminded.
Salviati states: I greatly doubt that Aristotle ever tested by experiment whether it be true that two stones, one weighing ten times as much as the other, if allowed to fall, at the same instant, from a height of, say, 100 cubits, would so differ in speed that when the heavier had reached the ground, the other would not have fallen more than 10 cubits.
This then marks the beginning of the modern era in science---the attitude that assertions about the
physical world by authorities, no matter how wise or revered, stand or fall by experimental test.
|
As an example of imprecise measurements, let's time gravity ...
Some Experiments with Gravity:
Galileo droppa da Big Cow
What is the main problem here with respect to determining experimental accuracy?
Like Galen, Galileo kept detailed records of his experimental procedure so others could duplicate it.
But, How to slow down gravity?
Translated Quote from one of Galileo's Journals:
A piece of wooden moulding or scantling, about 12 cubits long, half a cubit wide, and three finger-breadths thick, was taken; on its edge was cut a channel a little more than one finger in breadth; having made this groove very straight, smooth, and polished, and having lined it with parchment, also as smooth and polished as possible, we rolled along it a hard, smooth, and very round bronze ball. Having placed this board in a sloping position, by raising one end some one or two cubits above the other, we rolled the ball, as I was just saying, along the channel, noting, in a manner presently to be described, the time required to make the descent. We repeated this experiment more than once in order to measure the time with an accuracy such that the deviation between two observations never exceeded one-tenth of a pulse-beat. Having performed this operation and having assured ourselves of its reliability, we now rolled the ball only one-quarter the length of the channel; and having measured the time of its descent, we found it precisely one-half of the former. Next we tried other distances, compared the time for the whole length with that for the half, or with that for two-thirds, or three-fourths, or indeed for any fraction; in such experiments, repeated a full hundred times, we always found that the spaces traversed were to each other as the squares of the times, and this was true for all inclinations of the plane, i.e., of the channel, along which we rolled the ball. We also observed that the times of descent, for various inclinations of the plane, bore to one another precisely that ratio which, as we shall see later, the Author had predicted and demonstrated for them.
For the measurement of time, we employed a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results.