The Players in The Historical Development of Quantum Mechanics

The development of quantum mechanics was perhaps the greatest intellectual achievement of the 20th century.  While many individuals made contributions, twelve are highlighted in this abbreviated history.

Sir William Hamilton (1805-1865)
Hamiltonian Function
Had Hamilton, often considered the "forgotten founder" of quantum mechanics, been around in the 1920's, he surely would have seen the connection between matrix mechanics and wave mechanics.
The Hamiltonian function (1835) expresses rate of change in time for a set of moving particles. It specifies total energy (kinetic & potential) in terms of dynamics, position, and momentum of particles. Hamiltonians are a method for finding the minimum value of a given equation and are used to calculate the path of least action such as orbits and trajectories. Hamilton's unification of dynamics and optics has had a  lasting influence on mathematical physics, even though the full significance of his work was not fully appreciated until after the rise of quantum mechanics.

David Hilbert (1862-1943)
Hilbert Space
David Hilbert was one of the outstanding mathematicians of the modern era. He proposed 21 geometry axioms--the greatest influence in geometry since Euclid (325 BC).  Hilbert's work on infinite-dimensional space, later called Hilbert space, proved invaluable for quantum mechanics. Today quantum mechanics is said to be a theory set in "Hilbert Space."  At the InternationalCongress of Mathematicians in Paris (1900) Hilbert presented the now famous 23 problems which he challenged 20th century mathematicians to solve. In 1915 Hilbert discovered the correct field equations for general relativity before Einstein but never claimed priority.
As professor of mathematics at the University of Göttingen, outstanding scientists of the 20th century (Born, Heisenberg, Jordon, von Neumann to name just a few) studied with Hilbert. Hilbert suggested to Heisenberg that he find the differential equation that would correspond to his matrix equations. Had he taken Hilbert's advice, Heisenberg may have discovered the Schrödinger equation before Schrödinger. When mathematicians proved Heisenberg's matrix mechanics and Schrödinger' swave mechanics equivalent, Hilbert exclaimed, "Physics is obviously far too difficult to be left to the physicists and mathematicians still think they are God's gift to science."
 

Max Planck (1858-1947)
Quantum Theory
Most theoretical physicists usually do their most important work by the age of 25 (Newton, Einstein, Bohr, Heisenberg, Dirac, de Broglie, Pauli).  This seems to be the ideal age since there is time to learn enough while maintaining revolutionary ideas. What is remarkable about Planck is that at age 42, he explained the puzzle of "black body radiation."  Any object with a higher temperature than its surroundings loses heat by radiation. The hotter the object, the more radiation it produces. Since a black body absorbs all frequencies, it should radiate all frequencies equally.  Instead, black bodies emit larger quantities of some wavelengths than others. In 1900 Planck proposed that radiant heat energy is emitted only in definite amount called quanta.
           E = hn   n = frequency of light h = 6.626x10-34 J•s
Planck maintained that only certain energies could appear and were limited to whole-number multiples of hn.  Planck originally called h "quantum of action" since the product of energy and time is known as action (based on Hamilton's principle of least action).  Today h is known as Planck's constant and symbolizes the revolutionary new physics.
A young Max Planck was to give a lecture on radiant heat.  When he arrived he inquired as to the room number for the Planck lecture.  He was told, "You are much too young to be attending the lecture of the esteemed professor Planck."

Albert Einstein (1879-1955)
Photoelectric Effect
1905 was a good year for Einstein.  He managed to solve three of the outstanding problems of physics: the photoelectric effect, Brownian motion, and special theory of relativity.  These three publications have become known as the "Einstein trilogy."
Prior to 1905 researchers noted that current was proportional to the intensity of light striking the surface of a metal. The maximum kinetic energy of electron does not depend on intensity but rather on the frequency of the light. Einstein realized Planck's idea of light appearing as quanta (bundles) was the key to understanding this photoelectric mystery.  If the wavelength is short enough, the electron cannot escape. The important thing is the energy of the bundle and not number of bundles (brightness). The photoelectric effect is recognized as the first scientific work utilizing quantum mechanics.
Einstein could never accept some of the revolutionary ideas of quantum mechanics ("God does not play dice").  When reminded in 1927 that he revolutionized science 20 years earlier, Einstein replied, "A good joke should not be repeated too often." 

Niels Bohr (1885-1962)
Bohr Theory of Atom
Bohr (1913) was the first to apply the quantum theory to atomic structure. The most impressive result of the so-called Bohr theory was the way it accounted for the series of lines observed in the spectrum of light emitted by atomic hydrogen. Bohr was able to determine the frequencies of these spectral lines to considerable accuracy by expressing them in terms of the charge and mass of the electron and Planck's constant. To do this, Bohr also postulated that an atom would not emit radiation while it was in one of its stable states but rather only when it made a transition between states. The frequency of the emitted radiation would be equal to the difference in energy between those states divided by Planck's constant. This meant that the atom could neither absorb nor emit radiation continuously but only in finite steps or quantum jumps. It also meant that the various frequencies of the radiation emitted by an atom were not equal to the frequencies with which the electrons moved within the atom.  This was a bold idea that some of Bohr's contemporaries found difficult to accept.
In 1916 Bohr was appointed professor to the newly created chair of theoretical physics at the University of Copenhagen and in 1921 the Bohr Institute opened with Bohr as its director. The Bohr Institute became a leading center for quantum physics with young theoretical physicists from all over the world (Pauli, Heisenberg, Dirac, Oppenheimer, and Gamow to name just a few) coming to Copenhagen to work with Bohr.

Werner Heisenberg (1901-1976)
Quantum Mechanics
Making use of matrix algebra, Heisenberg (1925) developed a system called matrix mechanics.  It consisted of an array of quantities which when appropriately manipulated gave the observed frequencies and intensities of spectral lines.  The consequence of Heisenberg's work is his revolutionary (1927) uncertainty principle:  DqDp > h
The uncertainty of position (Dq) of an electron in an atom multiplied by the uncertainty of its momentum (Dp) must be greater than Planck's constant (h).  The uncertainty principle tells us that all observable quantities are subject to changes determined by Planck's constant and we cannot know position and momentum simultaneously. While a photon will not disturb an object like a house, it does alter position and momentum when bounced off an electron.
Heisenberg is out for a drive when he's stopped by a traffic cop. The cop says, "Do you know how fast you were going?"
Heisenberg says, "No, but I know where I am."
 

Louis de Broglie (1892-1987)
Wave Nature of Electron 
As an undergraduate de Broglie studied medieval history. During World War I he served in a field radio communication unit and this changed his interest from Gothic cathedrals to electromagnetic waves.  After the war de Broglie did his doctoral thesis in what has become known as "de Broglie waves." In 1924 de Broglie speculated that nature did not single out light as the only entity to exhibit wave-particle duality. He proposed that ordinary particles such as electrons could also exhibit wave characteristics in certain circumstances. de Broglie assumed that an electron has associated with it a system of "matter waves."  These waves possess crests that disappear at one point and appear an instant later at another point.  The distance between successive crests (l) is the de Broglie wavelength and it is calculated from l = h/mv, where h is Planck's constant and mv is momentum.

The following is taken from Thirty Years that Shook Physics by George Gamow:
At our first meeting we started talking physics although de Broglie did not speak any English and my French was rather poor.  But somehow I managed to convey to him what I wanted to say and to understand his comments. A year later I was in the audience in London when de Broglie delivered a brilliant lecture in perfect English.  Then I understood another of his principles: When foreigners come to France, they must speak French.

Erwin Schrödinger (1887-1961)
Wave Equation
Adopting the proposal by de Broglie that particles of matter have dual nature and in some situations act like waves, Schrödinger (1926) produced the basic equation of quantum mechanics.  The Schrödinger equation treats electrons as matter waves:

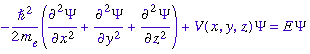
The only problem with Schrödinger's equation was his interpretation of the matter wave was wrong.  He described y as the density distribution--some regions rich in electron matter while others scarce.  But it was Max Born who figured out what the equation actually predicts.
In 1944 Schrödinger wrote a short book entitled "What is Life?" Schrödinger suggests that one of life's essential features is the storage of a genetic code passed from parent to offspring. Because it had to fit in a single cell, Schrödinger suggests the code is written at the molecular level. Schrödinger's book had a pronounced influence on Crick & Watson, discoverers of DNA. 

The following is taken from The God Particle by Leon Lederman:
Leaving his wife at home, Schrödinger booked a villa in the Swiss Alps for two weeks, taking with him his notebooks, two pearls, and an old Viennese girlfriend. Schrödinger's self-appointed mission was to save the patched-up, creaky quantum theory of the time. The Viennese-born physicist placed a pearl in each ear to screen out any distracting noises.  Then he placed the girlfriend in bed for inspiration. Schrödinger had his work cut out for him.  He had to create a new theory and keep the lady happy.  Fortunately, he was up to the task.

Max Born (1882-1970)
Probability Density
In 1926, after his student Werner Heisenberg had formulated the first laws of quantum mechanics, Born collaborated with him to develop the mathematical formulation that would adequately describe it. When Schrödinger put forward his quantum mechanical wave equation, Born showed that the solution of the equation has a statistical meaning of physical significance. Born's interpretation of the wave equation proved to be of fundamental importance in the new theory of quantum mechanics. Schrödinger believed that the electron was spread out in space and its density given by the value of y2. Almost immediately Born proposed what is now the accepted interpretation: y2 gives the probability density of finding the electron. The distinction between the two interpretations is important.  If y2 is small at a particular position, the original interpretation implies that a small fraction of an electron will always be detected there. In Born's interpretation, nothing will be detected there most of the time, but when something is observed, it will be a whole electron. The concept of the electron as a point particle moving in a well-defined path around the nucleus is replaced in wave mechanics by clouds that describe the probable locations of electrons in different states. Born's probability density is perhaps the most dramatic change in viewing our world since Newton and gravity.

The following is taken from Men Who Made a New Physics by Barbara Cline:
Born has been described as a moody and impulsive person.

However some of his quotes are quite telling:

Wolfgang Pauli (1900-1958)
Exclusion Principle
Pauli proposed a new quantum theory property (1925) called "two-valuedness."  Goudsmit and Uhlenberg identified this fourth quantum number as electron spin.  The exclusion principle is now stated as, "No two electrons in an atom can have the same set of four quantum numbers."
The exclusion principle subsequently has been modified to include a whole class of particles of which the electron is only one member. Subatomic particles fall into two classes: particles obeying the Pauli exclusion principle are fermions and all others are bosons. When in a closed system, such as an atom for electrons or a nucleus for protons and neutrons, fermions are distributed so that a given state is occupied by only one at a time.
Undergraduate Pauli moderated an Einstein lecture. After Einstein's response to a  question Pauli summarized with, "What Einstein says is not so stupid!"
When distinguished physicist Paul Ehrenfest told Pauli that he liked Pauli's publications better than he liked Pauli, Pauli replied, "That's odd, I feel the exact opposite about you!"

Paul Dirac (1902-1984)
Quantum Electrodynamics
Dirac laid the foundations for quantum electrodynamics (1927) with his discovery of an equation  incorporating both the quantum theory and the theory of special relativity.  Dirac showed that the correct relationship between mass and energy was not Einstein's equation (E = mc2) but actually E2 = m2c4. When solving Dirac's equation, E =mc2 as well as E = -mc2
But how can energy of an electron be negative?
Dirac predicted the existence of electrons with positive charge (antielectron or positron).  In 1932 Carl Anderson detected positrons.  Dirac also predicted every particle possesses an antiparticle (antiproton, antineutron, etc.).
Local Interest:  Dirac was professor of physics at Florida State University from 1971-1984.                 The Dirac Science Library is named after him.

During a question and answer period after a lecture Dirac gave at the University of Toronto, an audience member raised his hand and said, "Professor Dirac, I do not  understand how you derived the formula on the top left side of the blackboard."
"That is not a question," snapped Dirac, "it is a statement.  Next question, please."

John von Neumann (1903-1957)
Operator Theory
Early quantum theory had two approaches: Matrix mechanics proposed by Heisenberg and wave mechanics developed by Schrödinger.  Heisenberg found the physical ideas of Schrödinger's theory "disgusting," and Schrödinger was "discouraged and repelled"  by lack of visualization in Heisenberg's method.
von Neumann was considered the brightest young mathematician in Europe.  After hearing Heisenberg lecture on matrix mechanics, von Neumann decided to develop his own version of quantum mechanics--the matrices of Heisenberg were "too imprecise."  In his book (1932), The mathematical Foundations of Quantum Mechanics, von Neumann invented operator theory (now called Neumann algebras) to explain certain aspects of quantum mechanics.  Largely because of his work, quantum physics and operator theory can be viewed as two aspects of the same subject. von Neumann's new mathematics proved Schrödinger and Heisenberg theories equivalent mathematically. Schrödinger's wave mechanics eventually became the method of choice because it is less abstract and easier to understand than Heisenberg's matrix mechanics.
In 1933 von Neumann solved Hilbert's fifth problem, the case of compact groups. Although he never won Nobel Prize or gained world-wide fame, von Neumann was one of the truly outstanding mathematician/scientists of the 20th century.

1927 Solvay Conference

Held in Belgium, the conference was attended by the world's most notable physicists to discuss the newly formulated quantum theory