N = # of particles per cubic centimeter. Since
the particles are protons, to estimate N you divide the central density
of the sun (~150 g/cc) by the mass of a proton. This gives you
N = 1026
v = average velocity of proton: 1/2mv2 = 3/2kT; for T = 107, v = 4 x 107 cm/sec. (~.001c)
σ = cross sectional area for collisions. This is actually somewhat complicated but for simplicity we will just take the value of σ to be the surface area of a proton: σ = 10-26 cm2
So the collision rate, in units of collisions per second is then:
Although 3/2kT specifies the average kinetic energy of a proton, there clearly is some distribution of energies around that value.
The distribution of particle speeds in a gas follows what is called a Maxwell Boltzman distribution. That distribution is like a Gaussian but has a longer tail towards high particle speeds. Graphically, for the case of stellar interiors, that distribution looks as follows:
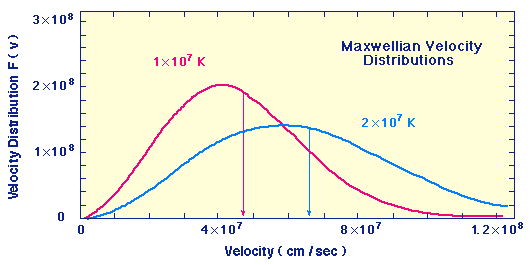
For a factor of two increase in temperature, the collision rate only goes up as Root 2, so the collision rate is not that sensitive to temperature.
The equation for a maxwellian velocity distribution is of the form:
or
e-v2/T
Since KT = 1 KeV and Ebarrier = 700 KeV (0.7 MeV), the probablity of particle having KE > Ebarrier is probability is e-700.
This is a lot smaller than the quantum tunneling probabilty derived earlier of e-22.
This is the basic reason that quantum tunneling must be invoked as the mechanism that allows protons to interact.
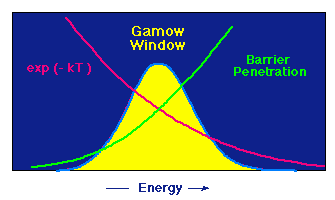
So we need quantum tunnelling as well and its really the convolution of the tunnelling probablity and the maxwell distribution of particle energies that yields the most probable range of proton kinetic energies that will start the fusion cycle.
This is called the gamow peak and its shown below. Your second homework assignment asks you to derive this peak energy.
