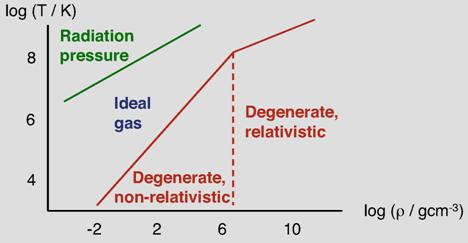
We now move into a discussion about degenerate matter. The most important physical aspects of a degenerate equation of state are

• The pressure is independent of Temperature
• Energy deposition/heating of a degenerate gas therefore does not lead to its expansion. Rather, it leads to increase momentum of the particles in the degenerate gas.

Degeneracy is a direct result of the Pauli Exclusion Principle

We can use the uncertainty principle in combination with the concept of phase space. Phase space represents the combined position and momentum vectors of a particle in N dimensions. In our case, N=3, so each particle has an X,Y.Z spatial direction as well as X,Y,Z components of its momentum vector.

Therefore, in general

[Δ X Δ Y Δ Z][Δ p_X Δ p_Y Δ p_Z] ~ h³

For a normal gas, the density determines the available volume in physical space and the temperature determines the available volume in momentum space. But this is not the case for a degenerate gas. We will see that density alone determines phase space volume.

For the specific case of an electron gas, only two electrons (of opposite spin state) can occupy a specific cell in phase space.

A specific cell would have coordinates:

x,y,x
p_x, p_y, p_z

To avoid being in that cell, the next pair of electrons will need to acquire additional momentum to create a new cell in phase space. Its this additional momentum which leads to increased pressure.

Now let's consider the case of non-relativistic degeneracy:

Let N_pdp = # of electrons having momentum (p) in the range p to p+dp. Consider a volume of 1 cm³.

The momentum volume element in this case is then 4π p²dp and N_pdp = # cells x 2 particles per cell.

If we want to find the total number of particles, then we have to integrate over momentum space, where the maximum momentum is p_o

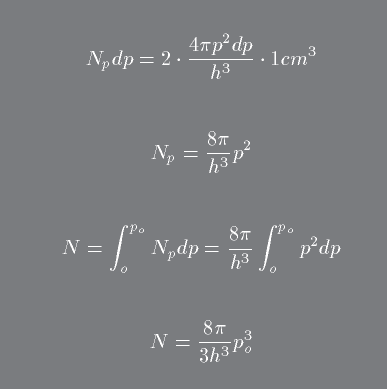
The physical meaning of the above is that all cells in phase are filled with partcles having momenta from o to p_o (known as the Fermi momentum).

Therefore, if the volume gets smaller (as the stellar core is contracting), p_o must increase.

We next want to calculate the pressure in this situation. Remember that pressure is the rate of momentum transfer.

An important point to note is that even though the gas is degenerate, the statistical behavior of the particle velocities is exactly the same as in an ideal gas law. That is, a Maxwell-Boltzmann distribution pertains. In that situation we then have the following:

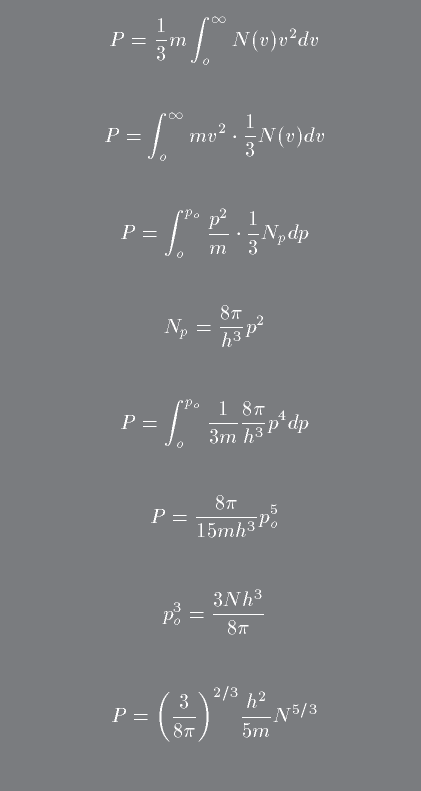
Now, note the following. As the core contracts, particle momementa must increase but it can not do so without limit. The limit is when the electron velocity ~ c, and in that case the gas is fully relativistic.

In this case, we have to put in the relativistic energy in place of mv² above. That means that the term p²/m goes instead to p/m and the resultant degenerate pressure will go as N^4/3 not N^5/3.

An interesting consequence of degenerate Pressure is the necessity of the inverse mass-radius relation. This relation for a degenerate core is such that if you add mass to a system of constant radius it shrinks, thereby increasing the density.

We can see this using two different approaches:

Hydrostatic Equilibrium

The Virial Theorem

In both cases we make use of scaling behavior.

The first case below is for Hydrostatic Equilibrium and the second on is for the virial theorem. Its important that you fully understand the power of examining scaling relations and their implications (this is also a good question for the midterm ...)

Note in the case of application of the virial theorem, the total internal energy, T, of a degenerate gas goes as its Volume times the energy density in the gas.

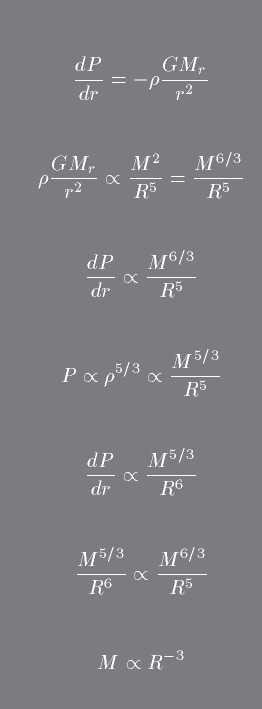
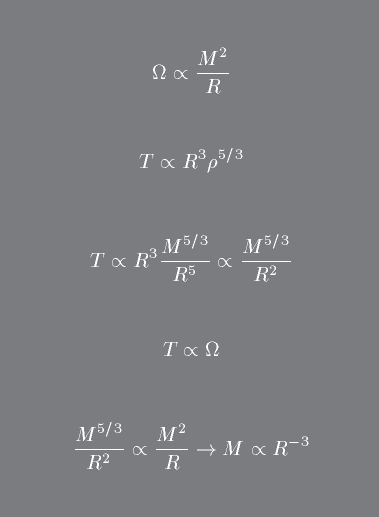
In the case of relativistic degeneracy, you should confirm that that you will get a scaling relation of the form:

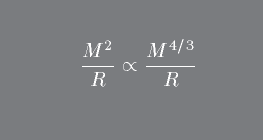
That is, there is some unique mass that is required for the relativist degeneracy limit. This is called the Chandresekhar mass.

Convenient scaling relations for white dwarfs and neutron stars are given below. In general, for a fully ionized electron gas, the mean mass per free electron is 2, so the second term on the right hand side becomes 1. In a partially ionized gas, which will occur as the degenerate core cools, the radius will adjust itself to a new value.