Assumptions:

• Our main sequence star is pure hydrogen

• we treat it like a classical and ideal gas such that the average kinetic energy per particle is
  E = 3/2 kT

  But what is T?

  Simple Estimate:

  From hydrostatic equilibrium we showed that:

  

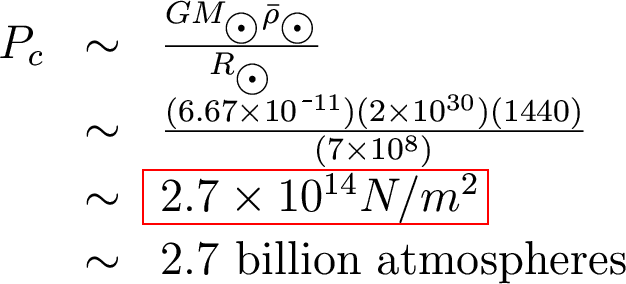
  And we apply the ideal gas law:

  

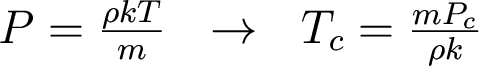
  If we substitue the hydrostatic value for P_c and assume constant density (which is wrong) in order for the density terms to cancel, our estimate of the central temperature becomes

  T_c ~ (GM/R)(m_p/k)

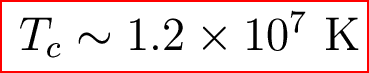
Using this estimate for core temperature leads to an average energy per particle of 1 Kev.

The ionization energy of hydrogen is 13.6 eV and therefore, in this environment, the hydrogen is completely ionized. The stellar core is therefore a dense gas of protons and free electrons. Free electrons scatter photons and therefore contribute to the diffusion of photons through the stellar core.

To make energy, something needs to fuse:

Aside:

Nuclear and particle reactions have to obey 3 laws of nature. These are:

• Conservation of Charge
• Conservation of Baryon Number
• Conservation of Lepton Number

We did the example of the decay of the free neutron in class to show how these conservation laws work. You should verify that step 2 shown above does indeed satisfy the conservation laws, which is why anti-matter must be created.

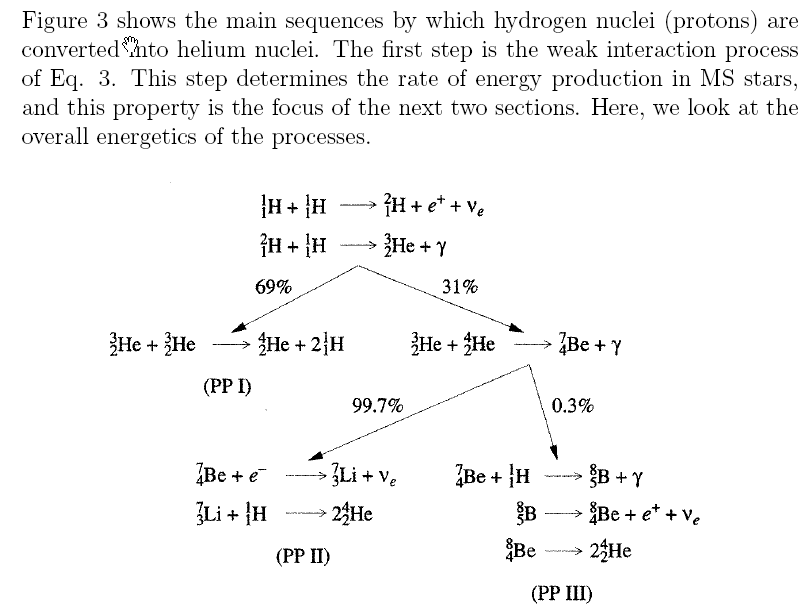
Utimately the first step of the fusion process leads to the conversion of Hydrogen to Helium in the core of a main sequence star. This is done via a process called the proton-proton chain (which we will summarize more fully on Wednesday Oct 12)

We calculate rest masses of nuclei in atomic mass units (amu), where one amu is 1/12 the mass of a carbon nucleus. In perhaps more useful units: 1 amu = 931.5 MeV/c²

In these units:

• mass of proton = 1.0078 amu
• mass of helium nuclei = 4.0026 amu.

  The change mass difference between 4 protons and 1 helium nucleus is therefore 0.0287 amu. The total energy release is thus:

  E = Δ mc² = 0.0287 * 931.5 MeV/c²* c² = 27 MeV (per reaction)

  Finally, the fraction of stellar mass which is converted to energy/luminosity is then:

  η = 0.0287/(4*1.0078) = 0.007

  Hence the available hydrogen mass can be converted into energy with an efficiency of 0.7%.

  But, Houston, we may have a problem with this simple view:

  Protons repel each other! Therefore the Coulomb barrier must be overcome. But this barrier is 0.7 MeV for protons. However, as we determined before, the average kinetic energy of the protons is 1KeV - a factor of 70 below what is needed for barrier penetration and then coupling via the strong force.

  Hence, classically, a proton at this average energy will never be able to get close enough to another proton to engage in either strong or weak interactions!

  Therefore, to understand why the sun produces energy, it is necessary to invoke barrier penetration using Quantum Mechanics.