ASTR 321 Third Homework Assignment

1. The ionization potential of hydrogen is 13.6 eV.

What is photon wavelength that corresponds to this energy
Using Wein's Law derive the equivalent blackbody temperature.
What spectral type star does this temperature most correspond to.

2. Find the effective temperature and luminosity of a main sequence 06 star.

Compute the number of ionizing photons by assuming that all ionizing photons have wavelength at λ_max and that the luminosity of star is essentially all radiate at λ_max
What is the radius of the corresponding stromgren sphere (in units of parsecs)?

3. Using a simple conservation of energy argument involving the kinetic energy of a particle compared to the potential energy of the universe, show that the critical density of the Universe can be expressed as: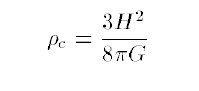

4. For a point mass object, show that the circular velocity of an orbit about that point mass declines as R^-1/2 where R is the orbital radius.

5. Our sun is located at a distance of 8 kiloparsecs from the center of the Galaxy and has an orbital velocity of 220 km/sec. Compute the orbital period of the sun around the galaxy as well as the mass of the galaxy enclosed within the orbit of the sun. Suppose we observe a star located at a distance of 80 kpc fomr the center of the Galaxy and it too has an orbital velocity of 220 km/s. Compute the mass of the galaxy based on that orbit and comment on whether or not a problem has arisen.

6. For a value of H = 75 km/s per Mpc, numerically calculate the critical density of the Universe in units of grams per cc. Compare that density to the density of a typical galaxy which as mass of 10¹² solar masses and a radius of 50 kiloparsecs (assume the galaxy is spherical).