Surface Brightness Selection Effects

The Tolman Test for the Expanding Universe:

Once upon a time, around 1930, there was still a debate about galaxy redshifts. To keep the Universe static (similar to the geocentric solar system model) an alternative theory of "tired light" (see this ).

The tired light hypothesis simply argues that the longer the travel time, the more photon energy is just lost and this gives rise to greater redshifts for more distant objects. Its a perfectly reasonable empirical hypothesis but it goes against fundamental physics (this is similar to MOND). So, if the tired light hypothesis is correct, then there is some photon-vacuum interaction which we don't know about.

In 1930 Tolman and later Tolman and Hubble (1935) came up with an interesting observational test that could distinguish between the expanding Universe hypothesis and the tired light/statci hypothesis.

Note that the geometrical difference between a static and expanding Universe is very large. A static universe is every euclidian. An expanding universe is curved but, more to the point, creates new space with increasing time. Therefore, a signal emitted by a distant galaxy was emitted at a time when the distance between that galaxy and a receiver was much less than the distance becomes at the time the signal is actually detected. This is due to the finite speed of light. In the static Universe there is no evolution in source-detector distance.

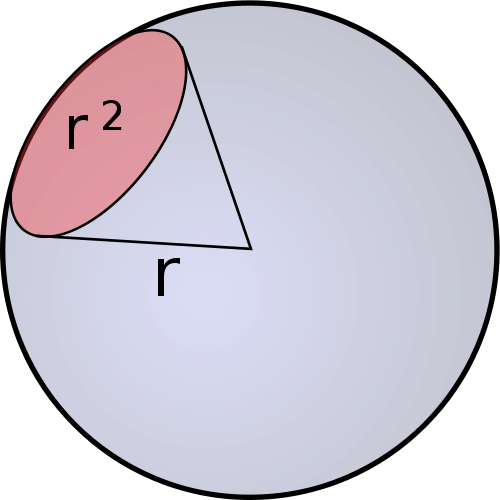
The surface brightness of galaxy in some bandpass (say a B filter) is basically the surface flux through some aperture.

The formal units of that flux are ergs per square cm per second per steraidan

If you take out the sterradian part, which is the solid angle of the object on the sky since its two dimensionsal see image below:

then this collapses to the the euclidian case.

But, in the expanding universe context, the redshift evolution of observed surface brightness is very strong.

a factor of (1+z) comes from time dilation -i.e. photons have to travel farther from distance to detector in expanding Universe.
another factor of (1+z) comes from the bandpass effect. Consider an object at z=1 measured through a filter of width 1000 angstroms. Well each angstrom is redshifted by an amount (1+z) = 2 in this case, so the received flux in that bandpass will be 1/2 that which was emitted (for an object with z = 1).
Two more factors of (1+z) come into the solid angle evolution of the source. The two factors come because the source is 2D. At the time the signal was emitted, the solid angle on the sky was simply much smaller than it is when the signal is emitted.

So the cosmological evolution of observed galaxy surface brightness goes as

(1+z)⁴
In a static universe it can easily be shown that surface brightness evolution would just go as (1+z).
In all galaxies have the same surface brighthness then this tolman test can be applied. Galaxies don't all have the same surface brightness but you can select samples that do and when you do, you find the data is far more consistent with an expanding Universe than a static one.
However, the (1+z)⁴ term is so strong that we know that the kinds of galaxies we see around us today can not be easily detected a large look back times because your the real signal (which is the surface brightness) starts to decrease to the level of the sky noise. For instance, at z = 2.5, SB would drop by about a factor of 100. This is the most serious selection effect in observational astronomy.

Galaxies are resolved objects that are imaged on some detector against a noisy background of finite brightness. Therefore, in principle, pixel to pixel noise competes with the signal of the galaxy for detection.
We define the surface brightness of the galaxy to be the luminosity that is enclosed within some area (as defined by an isophotal diameter ).
For a given detector and pixel noise there is a given surface brightness threshold above which galaxy light can be detected and below which the galaxy light is indistinguishable from the pixel to pixel noise on the detector.
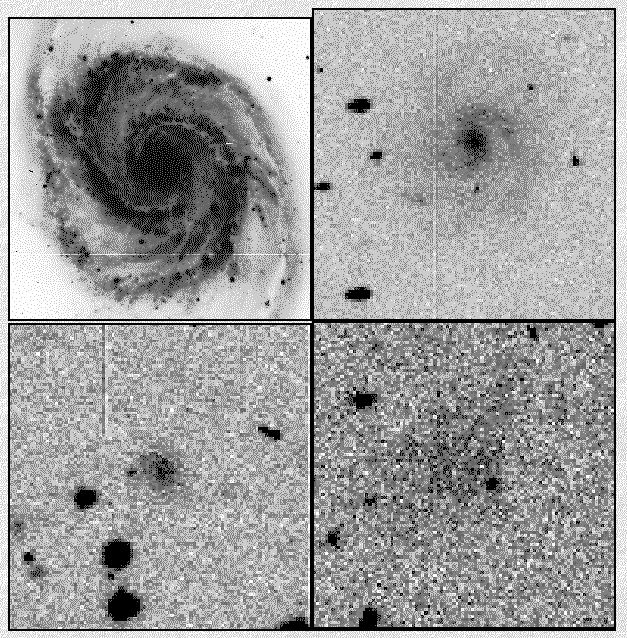
To make a very long story short, a class of Low Surface Brightness Galaxies, very diffuse galaxies with low constrasts or low S/N with respect to the night sky background, have been detected in large numbers. The following images show some examples and astrophysically, these objects are important because the a) show the observational selection effects exist, and b) most of the baryons in the Universe may be contained in these structures.