In many respects, understanding blackbody radiation is difficult statistical physics. We won't go there.

Instead, we will simply assume that a star is a dense object of finite temperature whose emission of radiation can then be properly characterized by the planck function. You may have seen this function before expressed in units of frequency

If you plot that function you get a characteristic curve whose peak only depends on temperature:

For simplicity, we assume the sun (or any star for the moment) to be pure hydrogen.

The mean density of the sun found from its mass (2x10³³ grams) and its radius (7x10¹⁰ cm) is 1.4 grams cm^-3.

The mean temperature gradient in the sun is approximately equal to the core temperature divided by the radius. The core temperature of the sun is approximately 15 million degrees (to be discussed in more detail later) which leads to a temperature gradient on the order of 10^-2 K/meter. This will become important later when we discuss the mean free path of photons in the solar interior.

Next we will demonstrate how integrating the planck curve shows that the total energy of a star depends on the fourth power of its blackbody temperature.

You integrate the planck function over all wavelengths, make a variable substitution to produce an integral that you can look up in a book and voila:

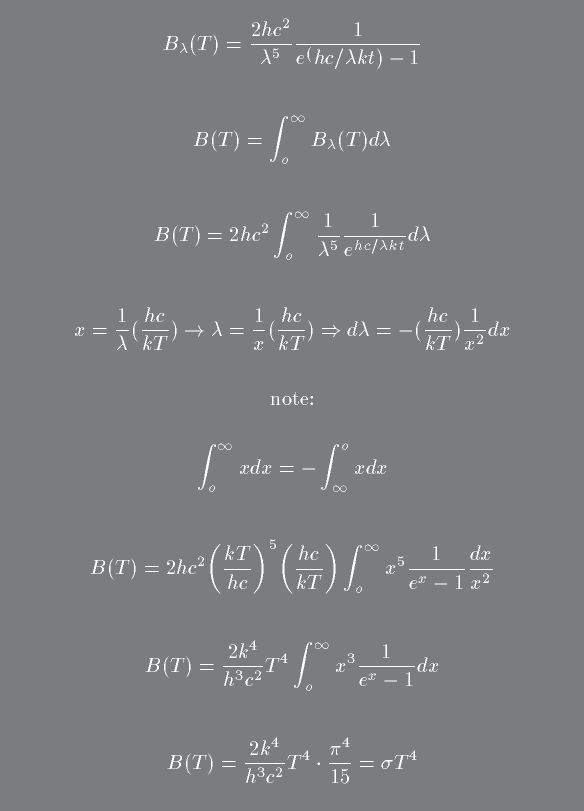
The planck function is an accurate description of the radiation given off by a dense object as long as thermodynamic equilibrium holds. Thermodynamic equilibrium represents a particular condition that holds between matter and radiation.

Under TE, the temperature of the matter and radiation are the same. The only way this can occur is if the radiation shares energy with the matter. This condition occurs whenever the radiation can not travel very far through matter without being absorbed or scattered. This condition is known as opacity

If you consider radiation passing through a slab or layer of material, the amount that radiation interacts with the material depends on three things:

• The total thickness of the layer (i.e. the path length through the material). dz

• The density of atoms in the layer ρ

• The absorption coefficient or cross-section of the atoms (which depends on chemical composition, degree of ionization, etc). This is usually denoted by the greek symbol kappa (κ) and its frequency dependent. The determination of this coefficient is one of the more difficult things to do in making a stellar model that is not based on pure hydrogen.

We can write the reduction in intensity, dI, as a function of these as follows:

dI/I = -κρ dz

Total absorption is set by the condition that dI/I = 1.

For a layer at about 1/2 a solar radius, κ = 1 (in cgs units) and we can take the density at this location to be the same as the mean density of the sun, which is about 1 as well.

Hence, at this layer, the mean free path of radiation is only 1 cm. This means a photon can not travel any more than 1 cm without interacting with the matter and then being randomly scattered by that interaction. Hence, photons diffuse through stars, they can not travel directly through them due to the very low mean free path. They do this by a random walk process of step length about 1 cm. The sun has R = 7e10 cm ~10¹¹ times larger than the step length.

Note that the above is oversimplified. In the very core of the sun the the mean free path of photons is closer to .05 cm than 1 cm. When you integrated over density in a real solar model you therefore find the diffusion time scale for the sun is about 10⁵ years instead of 10⁴ years.