The Stromgren Sphere Simple concept:

• A hot star is present (say T_eff of 50,000 K)

• it emits photons of wavelength < 912 A at a rate of N_u photons per second

• Each photon collides with one neutral hydrogen atom to produce an ionization. In this way, the gas surrounding the star is completely opaque to photons with wavelengths less than 912 A. An external observer would therefore never directly detect those photons.

• An entire volume, V , surrounding this star is photoionized.

• In this idealized gas, the volume is configured as a sphere

The cross section for ionization is very high: σ ~ 10^-17 cm²

This means that if the photon gets to within 10^{8.5 cm} for a proton, an ionization event will occur. 10^{8.5 cm} is about 3000 fm, or 3000 times the radius of a proton.

As an example: How far will an ionizing UV photon travel in an H I cloud with density of n_o = 1000 atoms per cc.

ΔR_s ~ (n_oσ)^-1 ~ (10³ cm^-3 * 10^-17 cm²) ~ 10¹⁴cm ~ 1/30000 pc or about 1 light hour. Therefore the ionizing photon quickly finds a proton.

Now let's think physically about what is going on. We just ionized a hydrogen atom thus creating a proton and a free electron. If that free electron immediately recombines with a proton, then nothing really happened. However, the density is very low and so there is some timescale (the recombination time scale) involved in when the free electron recombines with a proton.

As soon as the hot star has ionized some hydrogen, its opacity to ionizing photons becomes much larger, so the photons can travel further distances to ionize more of the H I cloud.

Thus the radius of the ionized sphere grows with time until an equilbrium between the ionization rate (which is function of the temperature and luminosity of the ionizing star) and the recombinbation rate. At that time, for every newly ionized hydrogen atom there is a newly created hydrogen atom from recombination. This is called a Stromgren sphere.

Inside this spherical volume, electrons and protons recombine at a volumetric rate:

r_r ~ α_Hn_en_p

where r_r is the number of recombinations per unit time in a unit volume (e.g. cm^-3 s^-1) and α_H is like a cross section for interaction (and has a value of 3 x 10¹³cm^-3 s^-1). n_en_p is the product of the number density of electrons and protons (which should be approximately equal at all times).

For example, what is the volumetric recombination rate if n_e= n_p = 10³ cm^-3?

r_r ~ α_Hn_en_p ~ 3 x 10¹³cm^-3 s^-1 * 10³ cm^-3 *10³ cm^-3 ~ 3x10^-7 cm^-3s^-1

We can express the recombination time (the time it takes for free electrons to recombine with protons) as:

τ = n_e/r_r ~ 10³/3x10^-7 ~ 3.3x10⁹ s ~ 100 yrs. This time scale is very short in comparison to the ionization lifetime of the star (at least 10⁶ years) that we readily expect the equilibrium to occur. In this equilibrium we can establish the following relations:

N_u = r_rV = α_Hn_en_p4/3 πR³_s

From which you can solve for the radius (assume n_e = n_p)

Notes: In most H II region environments there is not a lot of dynamic range in n_en_p - if the density is too low the photons have to travel to far to interact with a proton and equilibrium will not be reached.

if the density is too high then unless the star is extraordinarily hot, there will be an insufficient number of photons (obviously if N_u goes to zero than R_s goes to zero as well)

Example:

A star of spectral type O5 emits N_u ~ 6 x 10⁴⁹. For n_e ~ 1000 this leads to R_s ~ 1.2 parsecs. The mass of this H II region would be about 10₄ solar masses (the mass of the 05 star is about 20 solar masses). This is a typical H II region.

Now in reality, life is never this simple and star formation in GMC will likely produce many expanding H II regions which can run into each other and create shock fronts thus fostering a twisted mass of complexity:

Clearly the formation of massive stars can not hide. It will be evident in the recombination emission line spectrum and the primary optical emission line in this case is in the red (6563 angstroms) which is why most H II regions appear red.

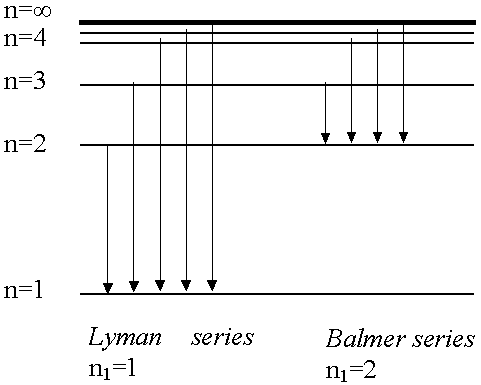
Therefore, if we can determine the H_α luminosity of some nearby galaxy we can in principle estimate what is current star formation rate is as that luminosity is a direct measure of the intergrated N_u produced in all the star forming regions in that galaxy.

For many disk galaxies, the spiral arm regions are where the star formation is occuring (within GMC complexes). If you produce an H_α image of a disk galaxy it often looks like what is shown below where the individual H II region complexes (each of the red areas is larger than a single idealized H II region) line up along the spiral arms.

As a consequence of active star formation, many galaxies exhibit an emission line spectrum in which H_α is the strongest feature:

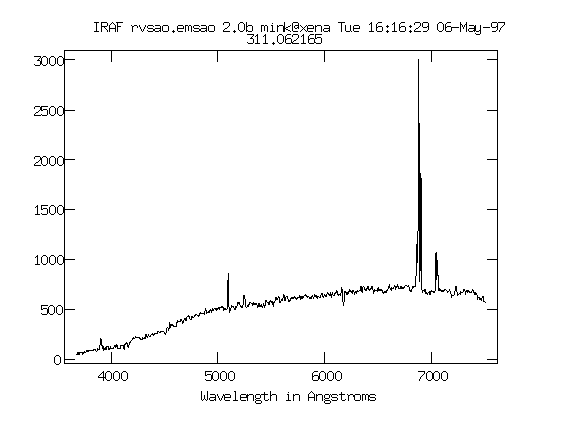
In 1912, astronomer V. Slipher using a spectrograph at the Lowell Observatory began to take spectra of "nebulae" - not knowing anything about the nature of these nebulae. One of these nebula was NGC 1068. This object has very strong emission lines that can be identified as emission from the Balmer series (as well as Oxygen emission).

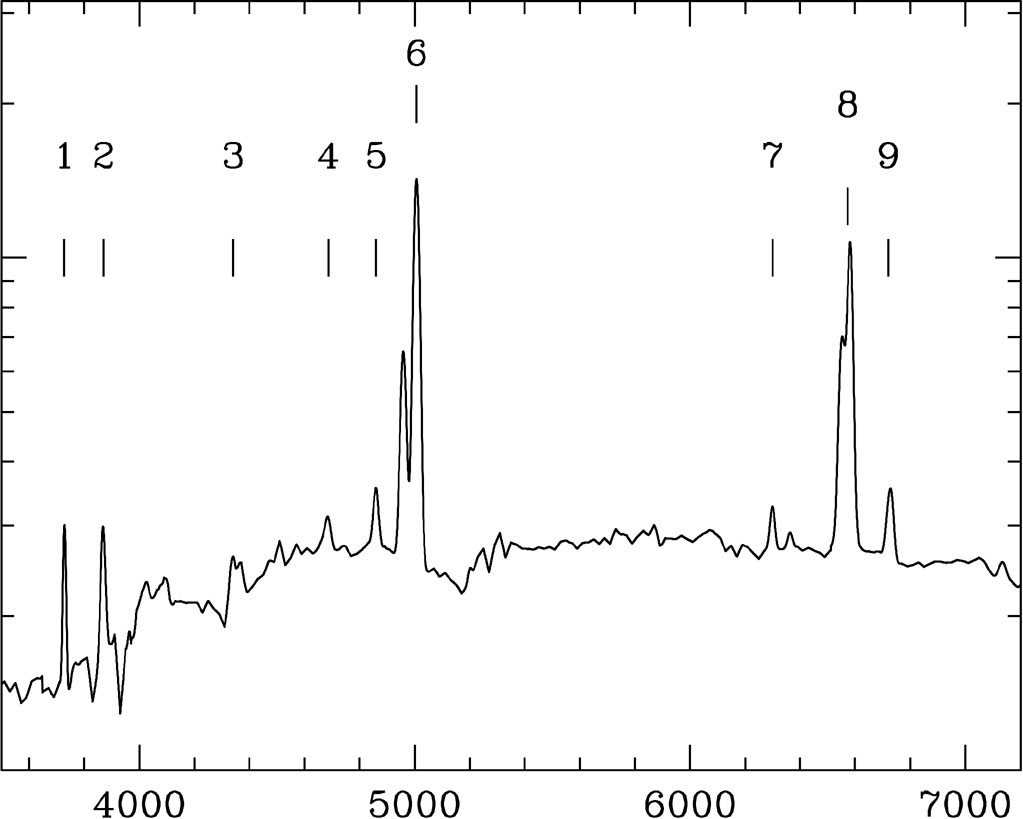
Slipher was easily able to identify the H_α line in the spectrum of NGC 1068 but noticed that the wavelength of this line was shifted by about 25 angstroms to a wavelength of 6588 indication that this object, NGC 1068, was moving away from us (at velocity of about 1150 km/sec). This was among the first set of measurements showing the redshifts of "spiral nebulae".