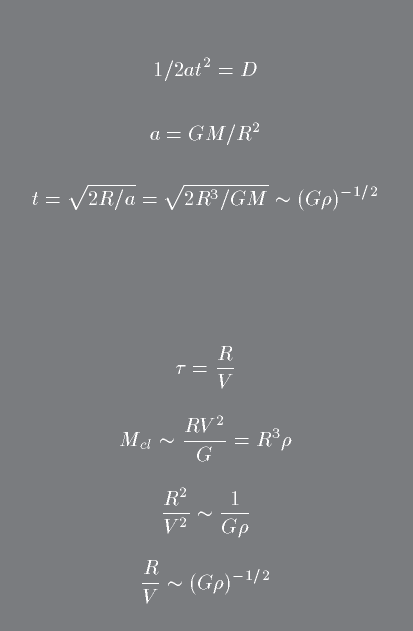When discussing the gravitational collapse of object it is useful to refer to a timescale, known as the dynamical timescale. This is the characteristic timescale of a system after which the virial theorem holds. Its universal in all kinds of systems and I will derive this timescale under three different scenarios:

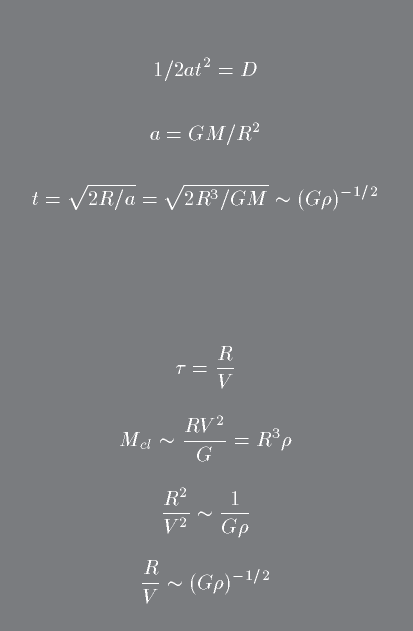
1) A pressure wave travelling through a hydrostatic fluid. Here we use the sound velocity as the characteristic velocity.

2) Gravitational free fall (or motion in 1D under constant acceleration).

3) Cluster crossing time. Here we equate the dynamical mass of the cluster with the mass obtained by considering it a spherical region of constant density.

These three cases are shown below in equation form.

Pressure Wave:

Free Fall and Crossing Time: