We will consider a star as series of shells of mass, each with mass dM_r . Within each mass shell, the density is constant. We will further assume that

a) Mass is conserved
b) The star is in pressure equilibrium (e.g. hydrostatic equilibrium)
c) The equation of state is given by the ideal gas law

Equation of mass continuity:

Since we do not know how the density varies with radius, we can not solve this equation. However, the form of this equation will be useful later on as a means of exchanging density and masses by using the ideal gas law as a mechanism to express density.

The most basic observation that can be made about the Sun is simple that it is a stable object. That is, its radius is neither expanding or collapsing. So independent of anything else we might now about the structure of the sun, we know that a basic equilibrium condition must prevail:

Hydrostatic Equiliubrium:

The above figure represents a slab of material, or, in our case, a shell of mass within the star.

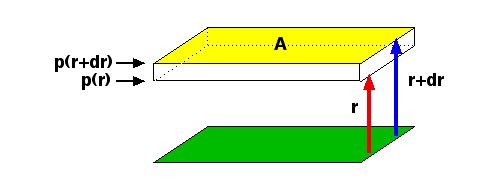
There is an upward force of gas pressure from the core temperature of the star on this shell.

There is pressure due to the combined layers of mass above the shell which is pushing the shell down. In addition, the shell has mass which is also producing a downward force of magnitude g dm where dm is the mass of the shell.

Remember that Force/area is a pressure. The area of the shell is dA and the pressure of the shell at radius = r is P and the pressure at radius r+dr = P+dp.

The density in the shell is assumed constant and the volume of the shell is just drdA.

Equilibrium occurs when the total downward force is balanced by the total upward force.

So,

Now we are in a position of estimating the central pressure of the sun. Lets consider a point which is at 1/2 a solar radius. At this point we will take the density to be the mean density of the sun (e.g. 1.4). We can now integrate over the limits R to R/2 where we take the pressure at r=R (e.g. the surface pressure) to be zero:

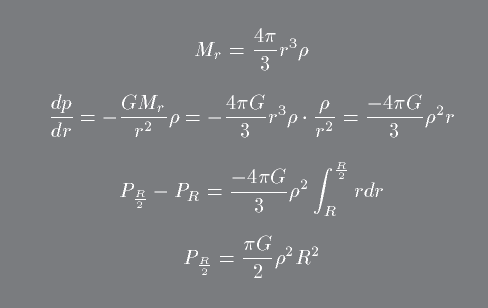
Taking R = 7 x 10¹⁰ cm then yields a Pressure of 10¹⁵ dynes cm^-2 which is the equivalent of about 10⁹ atmospheres.

Hence from simple principles and application of the ideal law (pressure is proportional to temperature) we now know that the interior layers of a star must be extremely hot.

Next time we will estimate what these temperatures are. From that, we can can insight into what the energy source for stars must be.