In Stellar Astrophysics we will use the ideal gas law as expressed in this form:
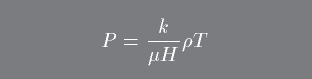
In Stellar Astrophysics we will use the ideal gas law as expressed in this form:
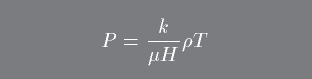
Where mu is the mean molecular weight which is the average atomic mass per particle (H = mass of the hydrogen atom). To see how mu differs under different situations, consider the following simple example.
A neutral hydrogen atom has a mass = H and is just one particle.
Ionized hydrogen still has a mass of H (because the mass of a proton is 1850 times that of an electron), but now there are two particles, so the average mass per particle is H/2.
Fully ionized hydrogen therefore has mu = 1/2. (a fully ionized gas of purely heavy elements has mu = 2 so, to within astrophysical accuracy, mu can always taken to be 1).
If we put our previously derived Pressure of 109 atmospheres into the ideal gas law, we derive that T = 5 million degrees at the layer R/2 for the sun.
Therefore, hydrostatic equilibrium considerations necessarily lead to
high temperatures in stellar interiors. The higher the mass, the greater the inward applied
force, meaning that a larger pressure and larger temperature are needed for balance. Higher masses
therefore create higher interior temperatures.