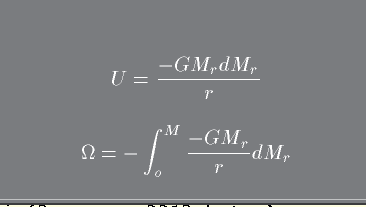
The first source of energy generation that was considered for stars (by Lord Kelvin) was simply the converstion of gravitational potential energy into radiant energy. This process works in the following manner:
We start by expression the gravitional potential energy associated with a shell of mass dMr . The total amount of potential energy comes from integrating overall mass shells.
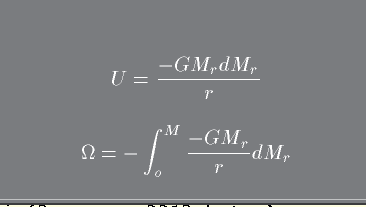
To find an expression for the Total kinetic energy, T , we integrate over the star using the average value of kinetic energy per particle (e.g. 3/2 kT). Note that dN = the number of particles in a thin mass shell of mass dMr .
This will allow us to write the Total kinetic energy in units of radii and density when we also use the equation for hydrostatic equilibrium.
We now want to integrate this equation by parts. If you can't remember integration by parts, the rule is:
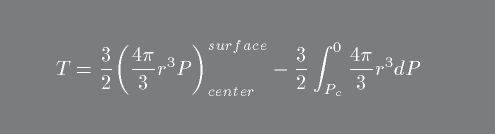
The first term is zero 
P = 0 at the surface and R =0 at the center.
We now use the hydrostatic condition to get rid of the dP (remember there is a minus
sign dp/dr = -gρ) and then
use the continuity of mass equation to get rid of the density term that necessarily
comes from using the hydrostatic equation and replace g using:
In addition, we need to get our intergal
over Mass and dMr to directly compare with the expression for Ω so going from line 1 to line 2 makes use of this subsitution:
You will now note that this expression for the kinetic energy, T is now exactly equal to -1/2 the expression derived earlier for Omega, the total gravitational potential. This is the virial theorem.
If we consider the sun as contracting from some initial radius to its current radius, then the change in gravitional potential is
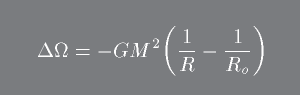
Half of that change is available as luminosity for the sun.