How fast will Resource X be depleted?

Well suppose we have the following situation:

• As of 2008, there are 100 units of Resource X still available to us
• In the year 2008, we will use 1 unit of Resource X.
• as measured over the last 6 years, our use of Resource X grows at the rate of 5% per year.

Dear Congressperson, when will resource X run out.

Congressperson says "oh don't worry, Resource X will be around for 100 years"

Really .... don't we use resources like rabbits?

70/n years; n =% growth rate

Its important to recognize that even in the slow growth period, the use of the resource is exponential. If you fail to realize that, you will run out of the resource pretty fast.

The correct equation for calculating the exponential exhaustion timescale of any resource (should be required knowledge for any one elected to congress):

T_e = 1/k * ln (Rk/r_o +1)

where k = growth rate
R = total resource available
r_o = initial consumption rate

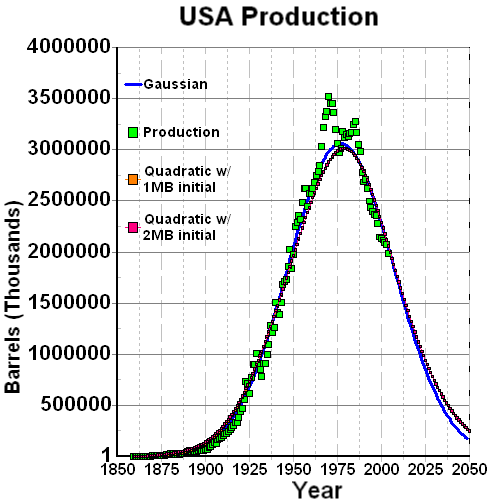Let's start out with the curve for US Oil production. Note that peak production occurs on a timescale of 1/2 of T_e as the production curve is assumed to be symmetric. When resources reach peak production, prices tend to go up which can then serve to lower consumption and extend the exhaustion timescale.

In 1956, M. King Hubbert published an ignored paper based on this methodology as applied to US Oil production.

• Measured Growth rate of oil production in the US over period of 1945-1955 was 3% (.03)

• Starting period of calculation is 1946

• Hubbert estimates the ratio of R/r_o in 1946 to be 120

• From this, what do you find as the year of peak production? Excel template

Other Examples to do in the Excel Template

Top 10 World Resource Usage (in units of millions of short tons per year - year 2005)

1. Coal 5186 electricity generation R/r = 175
2. Petroleum 3569 fuel for vehicles R/r = 40
3. Natural Gas 3355 heating; electricity generation R/r = 60

   
   
   

   

   
   
   

4. Iron Ore 1157 buildings; roads; infrastructure R/r = 250
5. Salt 205 whatever; who cares
6. Phosphate 157 fertilizer R/r = 80 Africa
7. Bauxite 139 aluminum production R/r = 125
8. Gypsum 106 sheet rock; fertilizer R/r > 20,000
9. Sulfur 60 industrial products; ferilizer (not mined; derived as a by-product from petroleum operations)
10. Manganese 26 production of steel R/r = 26 Market Reaction!
    US production Drops to Zero





So on the surface, application of Hubbert's methodology strongly suggests that the world is going to experience peak production on a variety of fronts. Various economic corrections will then occur.

Back to Congress:

The basic problem is that we substitute Disney's First Law for this arithmatic reality of resource depletion.