The Exponential Distribution

The exponential distribution can be used to model a Poisson process.

This can apply which some object, initially in State A, can change to state B with one constant probability per unit time.

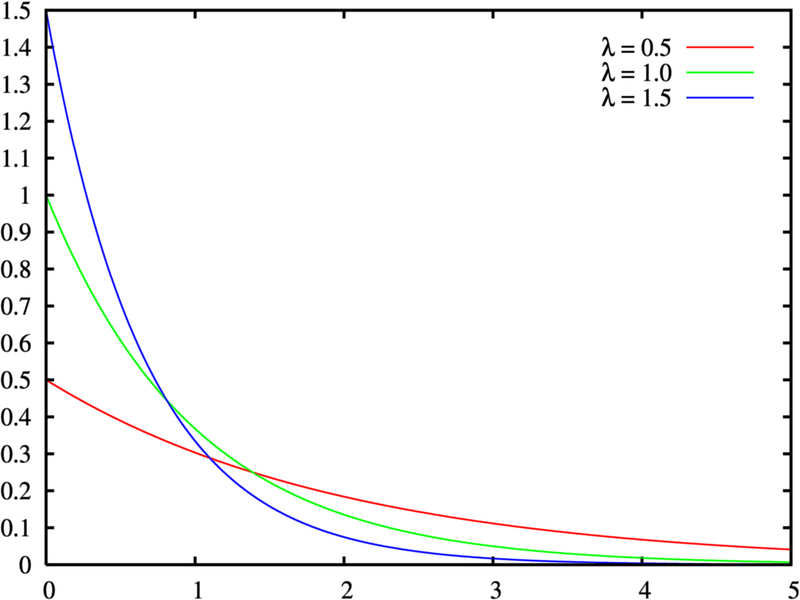
The time at which the state actually changes is described by an exponential random variable with parameter &lambda . The graph above is essentially a plot of the probability that the object has remained in state A as a function of time step, for various values of &lambda .

In effect, the exponential distribution describes the time for a continuous process to change state.

In real world scenarios, the assumption of a constant rate (or probability per unit time) is rarely satisfied. For example, the rate of incoming phone calls differs according to the time of day. But if we focus on a time interval during which the rate is roughly constant, such as from 2 to 4 pm during work days, the exponential distribution can be used as a good approximate model for the time until the next phone call arrives. Similar caveats apply to the following examples which yield approximately exponentially distributed variables:

• the time until you have your next car accident;

• the time until a radioactive particle decays, or the time between beeps of a geiger counter

• the number of dice rolls needed until you roll a six 11 times in a row

• the time until a large asteroid ( strike causes a mass extinction event (mass extinction event: an extinction event

Exponential variables can also be used to model situations where certain events occur with a constant probability per unit distance:

• the distance between mutation on a DNA strand;

• the distance between roadkill on a given street;