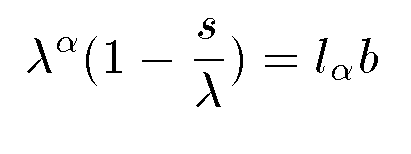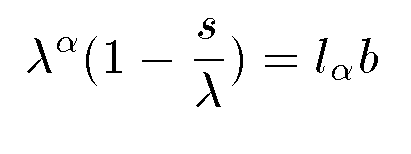So far we have discussed growth rates in fairly ideal terms. For instance, we have not really considered the case of finite lifetimes and survival probabilities.

Now we will.

For mammals to reproduce and the population grow or be stable, the following conditions have to be met:

• A Female mammal has to be born

• There is some probability that female will survive to fertility and have offspring

• Some of those offspring have to be females.

All of these conditions can be put together into a particular form for the growth rate.

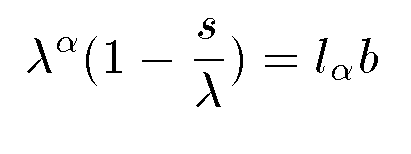
The terms in the above equation are the following:

• λ = the fractional growth rate per year for a species:
  • for a stable species λ = 1
  • values of λ less than 1 lead to population crashes. For instance a value of λ = 0.98 means the species population is declining at the rate of 2% per year (this is an exponential decline, of course).

• α = the age (in years) at which the species starts breeding

• s = the adult annual survival probability (in percent)

• b = adult average female fecundity - fecundity means the power of a species to multiply rapidly or its capacity to form reproductive elements. It is one measure of fitness.

  More explicitly b is average reproductive rate of female offspring per adult female in the overall population per year.

  So, if on average a female gives birth to another female once every 4 years, then b = 0.25.

• l_α represents the probability that a new born will survive to age alpha (the breeding age).
  note that l_α in turn = s_o * s₁ * s, where:
  • s_o = survival probability at birth and in fledgling stage of life
  • s₁ = sub-adult annual survival probability,
  • s is the adult annual survival probability

  Note that, of course, s, must be correlated at some level with s_o and s₁.

Environmental alteration and/or habitat loss basically directly influence l_α as that would impact values for s_o and s₁ more than anything else. Generally speaking, in mammalian populations, if you manage to survive to adulthood your basically likely to survive long enough to breed.

Hence species survivability or stability depends on how well the growth equation shown above can be optimized. Things that help species are:

• low values for α
• high values for b (note that b and &alpha are correlated; low values of α in species are accompianied by high b values)

• high survival probabilities

Conversely, environmental alterations that can trigger a population crash are

• stimuli that lower b (hard to do)
• habitat loss that lowers l_α (easy to do)

So this kind of growth equation (which is numerical in nature, that is, not analytic (solvable)) can be used to apply to populations with known or estimated survival rates, birth rates, and fertility ages. But something is missing from this framework. What is it?