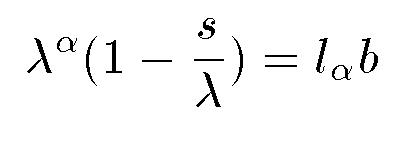
Due on Wednesday May 30
The Spooky Tooky is a large owl-like creature that tends to inhabit and mate in Old Growth Forest. The Spooky Tooky was once abundant in the wilderness but with the coming of the chain saw, the Spooky Tooky population is starting to dwindle. The Spooky Tooky population is important to the overall health of the ecosystem since they prey on the spineless manga toad that likes to suck the sap out of old growth trees, thus causing them to fall over, dead.
In addition, the Spooky Tooky can perform barrel rolls and loop to loop on command for the the entertainment of tourists visiting our National Forests. Thus, there is a keen need to develop effective policy to preserve the Spooky Tooky.
At last count, there were 12000 individual Spooky Tookies known. They are known to be long lived creatures and Sparky, the best known of all Spooky Tookies, is at least 60 years old (a.k.a. Sr. Tooky).
The Spooky Tooky, like most creatures in the forest, mate and produce offspring. Preservation of the Spooky Tooky then requires a habitat which a) lets them mate b) lets them have female offspring and c) lets the female offspring have a reasonable probability of living long enough to mate and have more female offspring.
The Spooky Tooky long ago discovered the Viagra tree and even old Sparky can still produce offspring. For a species like the Spooky Tooky, it can be shown that the geometric growth rate of the population can be approximated by the following equation:
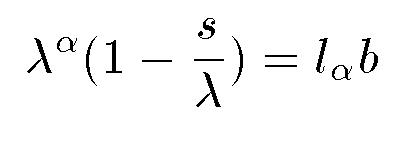
The terms in the above equation are the following:
Given a value of &lambda, we can then estimate the characteristic timescale of the population crash as

where N is the number of known individuals in the population (12000) in this case.
Below are three sets of data that have observationally determined the necessary parameters.
Your first task is to derive estimates of &lambda and &tau (the population crash time) from each of these data sets.
Data Set 1 (from University biologists):
Data Set 2 (from the Government Study)
When a group of university biologists went to the Spooky Tooky policy hearings, they were met by an angry mob of legislators that a) complained that university professors are overpaid and b) that they had done their study wrong by implicitly assuming that the Spooky Tooky, if they survive as an adult, lives for a very long time. Even though the biologists had Sr. Tooky with them, the legislators refused to believe that ol Sparky was really 60 years old.
The legislators then whipped out a formula produced at the Institute for Scientists that Whip out Formulas in which a new parameter w is now introduced. This parameter represents the maximum age for survival and reproduction. This whipped out formula is even more horrible that the first one:
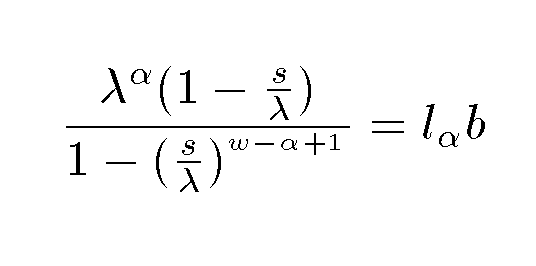
The republican legislators insist that w = 10 years while the democrats insist that w = 15 years. Using these values of w your third task is to use the three data sets to re-estimate values for &lambda and &tau and to explain why your results are sensitive to this new parameter.
Lastly there is the important question of equilibrium occupancy in Old Growth territory. In general, a species will not inhabit all of the available habitat as that would lead to extinction.
A working model is that habitable and uninhabitable patches of land are randomly dispersed throughout the forest ecosystem. This model makes an important prediction for po which is the equilibrium occupancy of suitable habitat by females (the model assumes the males will find them ...) and it has two parameters h is the proportion of the region which is habitable and k is the demographic potential of the species. Demographic potential is the equilibrium proportion of total territory that would be occupied by females in a completely suitable region. k is not something easily measured but po and h can be. These are related by the following:

For simplicity we will use now use p for po If h is known exactly (which we will pretend that it is) then the variance in k can be determined as follows:

Below are three data sets each with Np = 10.
Data Set 1 (from university biologists):
Data Set 2 (from the Government Study)
Your last task is to use this data to do the following for each of the three data sets