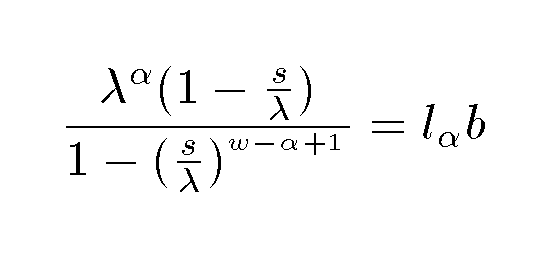
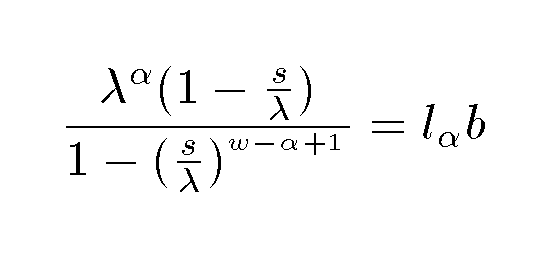
So, can we apply this equation to humans?
What do we know? Well we know that since the population is exponentially growing, that &lambda must be greater than 1, for humans.
Note tho, a mathematical oddity - S ≠ λ in this equation because then we will be dividing by zero
Also how should we interpret w?  maybe have w be the maximum age for female
reproduction?
maybe have w be the maximum age for female
reproduction?
Download the spreedsheet for this activity and do the following 3 exercises:
So in the spread sheet first set λ to something between 1.01 and 1.02 and then adjust the other parameters until cell M2 (the difference between the LHS and the RHS is close to zero). Note that you should be able to get within less than 0.001 for this difference.
 What are the implications of this solution?
What are the implications of this solution?