Noisy Data

In general, most environmental data has a considerable amount of random noise it. The origin of this random noise is

1. the phenomena itself has a lot of intrinsic variability - this is especially true with climate data

2. the measurements are often difficult and imprecise

The example below shows a time series where the intrinsic variability completely swamps out any potential trend. To identify possible trends it is necessary to smooth the data.

A variety of techniques exist for this.


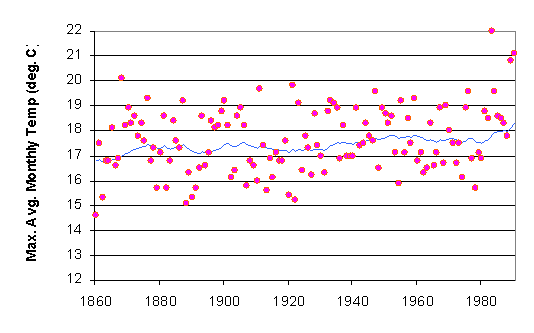
(blue line = smoothed trend)

Any data that has significant flucutations as a function of time may dominate the underlying wave form (trend with time). You therefore want to dampen out the fluctuations to reveal the underlying wave form.

The most common technique available is "smoothing". These techniques serve to surpress the noise and to extract real trends and patterns.

Note that smoothing and averaging are not the same:

• Averaging ends up with fewer actually data points
• Smoothing preserves the number of data points but lowers the amplitude of the noise by coupling the data points.

Techniques:

• Boxcar smoothing or sliding average: this works best when there is some underlying waveform to the data (long period systematics vs. short period fluctuations) (Note that the Excel function of "moving average" is, in fact equivalent to boxcar smoothing).

• Box Averaging: Replace N data points by the average of those data points. So suppose you have 100 data points and you average them in groups of 3. You will then up with 33 data points.

  Climate example

• Exponential Smoothing:
  
  
  Here the smoothed statistic, s_t is the weighed average of the previous data value (x_t-i) and the previous smoothed statistic, s_t-i; α is the smoothing factor (a value between 0 and 1).
  
  This method is often applied to data which has lots of short term fluctuations in it. Financial or stock market data is often treated this way but climate time series also lend itself to this smoothing approach.

  The functional form of this smoothing is governed by one parameter, the smoothing parameter, and it has a value between 0 and 1. Values close to one have less of a smoothing effect and give greater weight to recent changes in the data, while closer to zero have a greater smoothing effect and are less responsive to recent changes. There is no formally correct procedure for choosing the smoothing factor -its a scientific judgement call.

  Example excel spreadsheet (cell K1 is the only thing to change and is the smoothing parameter)

• Guassian Kernel Smoothing: This is very well suited to time series analysis.
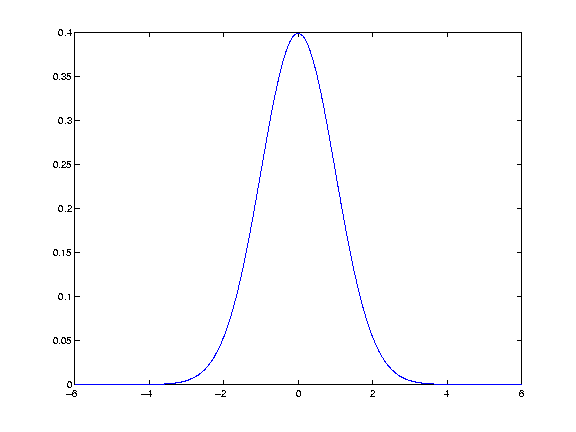  The 'kernel' for smoothing, defines the shape of the function that is used to take the average of the neighbouring points. A Gaussian kernel is a kernel with the shape of a Gaussian (normal distribution) curve. Here is a standard Gaussian, with a mean of 0 and σ (=population standard deviation) of 1.
  
  The basic process of smoothing is very simple. We proceed through the data point by point. For each data point we generate a new value that is some function of the original value at that point and the surrounding data points
  
  
  
  
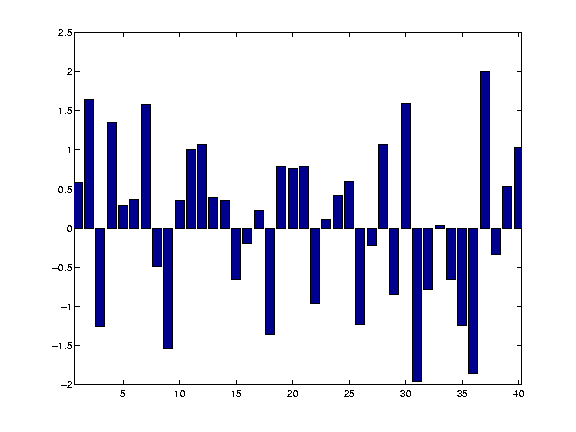
  For an example, let's say we want to replace the 14th value in our data set with a smoothed value.

  We have chosen our kernel to have standard deviation of 2.5 units on the X-axis. With the kernel centered x=14 and scaled so that the total area of the Kernal = 1 (this is required) our smoothing function now looks like this.
  
  
  
  

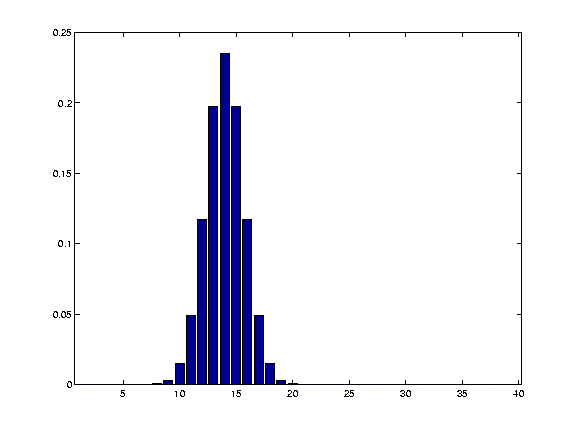  The discrete version of the function is shown at the left. The table below summarizes the x,y values of the function as well as the actual data.

  X	Y	Y-data
  12	0.117	1.065
  13	0.198	0.389
  14	0.235	0.349
  15	0.198	-0.656
  16	0.117	-0.195

  Note: we used a gaussian kernel with σ = 2.5. The example used here just uses the first 5 points (eg. ~ +/- 1 σ) which represents 86.5 % of the total area and so contains most of the weight in the smoothing (but you really do want to use all of the kernel to get the best results)
  
  
  
  
  We want to produce a new value for x = 14 based on this weighted smoothing function. That means we convolve our function with the data. That sounds onerous, but its really quite simple and works like this.

  The new Y-data point at X=14 is then:

  0.117*1.065 + 0.198*0.389 + 0.235*0.349 + 0.198*-0.656 + 0.117*-.195

  = .125 + .077 + .082 - .130 - .023 = .141 (compared to the actual data value of .349).

  We then apply the same procedure to point 15 etc and end up with a convolved time series distribution that looks like this, where larger scale patterns are now more evident

  

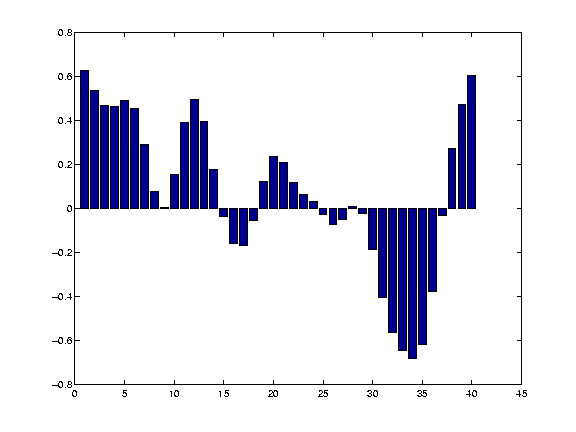
  This particular method is very good for image or pattern recognition and can be important for analyzing climate data:

  The "lab" exercise for this will involve analysis of the rate of Arctic Sea Ice Loss . This is a very big deal as it changes the planetary albedo should it occur.

  
  
  One of the things you will be asked to do in the lab exercise is feature extraction:
  
  Feature Extraction in noisy data. This is highly useful and involves baseline subtraction to produce what is known as a "flattened spectra". While these is an easy procedure for features of high singal to noise, in the world of climate data there may be decadel features that are importnat but have overall low S/N and therefore are not properly recognized.
  
  Visual Example:
  
  The most important part of dealing with noisy data is to produce a visualization (a graph) in which you can see the noise:
  
  

  
  
  Fitting a cubic spline - most often used technique. Here we have not windowed any features
  
  
  
  Now we window possible features and then fit cubic spline with those data values (within x-range of the window) not included.
  
  
  
  
  
  Subtract that polynomial baseline from every X-value to produce the flattened spectra:
  
  
  
  
  
  Is this just noise? Well, smooth the flattened spectra
  
  
  
  
  • Determine the RMS noise with the feature not included (it obviously will be less). In the case shown you would determine the rms noise (that is actually the same as the standard deviation) for the data from about x= 1 to 40 and from 90 to 106 as shown in the rectangles above.
    
    
  • If the peak value is at least 5 times the value of this noise, then your feature is real (its a statistical signal). For this example the Peak to Noise ratio is about 0.5/0.07 ~ 7