Population dynamics a good example of non-linear feedbacks in ecosystems.

Biologists like to talk a lot about r-selected (growth selected) and k-selected (carrying capacity limited) species usually in the context of predator-prey relations.

More specifically:

K-selected species usually live near the carrying capacity of their environment. Their numbers are controlled by the availability of resources. In other words, they are a density dependent species. Food availability is one resource that controls population size, especially if the food is relatively localized.

The attributes of a K-selected species include a long maturation time, breeding relatively late in life, a long lifespan, producing relatively few offspring, low mortality rates of young, and extensive parental care. Examples of a K-selected species include elephants, apes and humans.

The attributes of a r-selected species include a short maturation time, breeding at a young age, a short lifespan, producing many offspring quickly, small offspring, high mortality rates of young, and nonexistent parental care. Examples of r-selected species include waterfleas, insects, and rabbits.

r and K selection may depend on ecosystem condition:

• Organisms that live in stable environments tend to make few, "expensive" offspring. Organisms that live in unstable environments tend to make many, "cheap" offspring.

• Extreme r-strategists, such as the oyster, lose most of the individuals very quickly, relative to the maximum life span for the species. So they must reproduce fast to survive.

• Extreme K-strategists, such as humans, most individuals live to old age (again relative to the maximum life span for the species) and thus the population continues to build until some ecosystem carrying capacity is reached (then catastrophic collapse?)

While r vs K selection is a useful framework it generally oversimplifies the problem. Most real systems are subject to non-linear or chaotic dynamics, involving unstable oscillations around points of equilibrium.

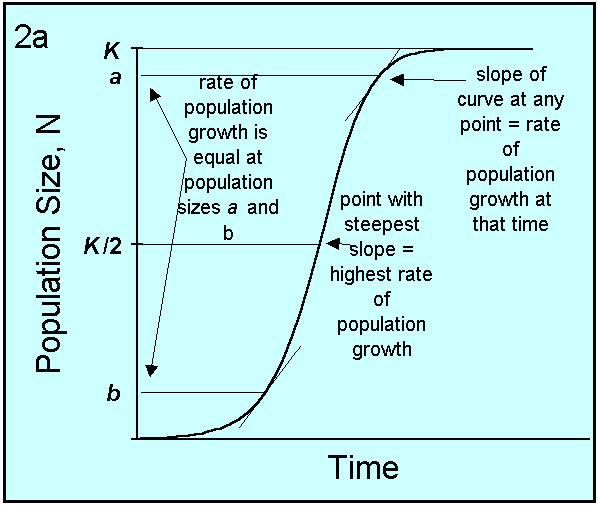
K-selected species are idealized by the equation below where it can be seen that the growth rate, R, becomes zero as N approaches K. This is called negative feedback - the idea being as conditions get "crowded" it is detrimental to growth. The problem with real systems is that estimates of K are very difficult and uncertain:

Note when N << K, N/K is zero. In this case pure (unbounded) exponential growth is occuring:

(Note: Despite what you may have heard in other ENVS classes, human growth is occuring in a mathematically exponential way, on a logistic growth curve - this represents bounded exponential growth)

r-growth is standard exponential growth which leads to population crashes. The functional difference between r and K selected growth is shown below:

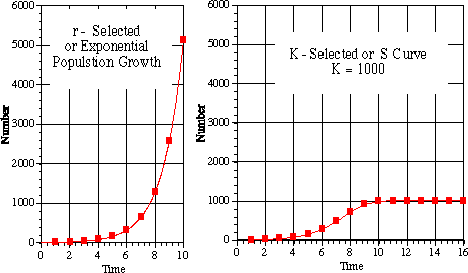
In reality, K-selected growth qualitatively looks like this:

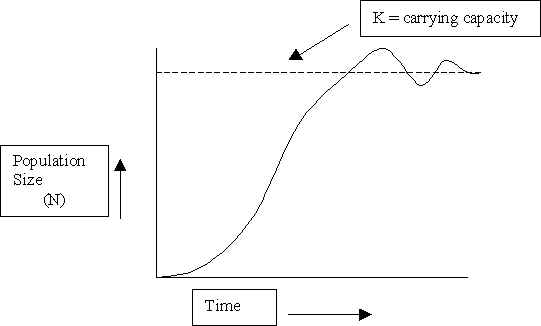
In this case we have r-selected growth up to the carrying capacity line but then we have oscillations about that line. These oscillations have points of unstable equilibria (i.e. the smaller scales peaks and valleys). Small perturbations in the system, when species growth is at one of these points, could trigger catastrophic continued r-growth or rapid decay. This is called non-linear dynamics (sometimes called chaotic dynamics).

Let's try an example with US population growth

In non-linear dynamics, small perturbations in some system can cause large changes in overall system evolution.

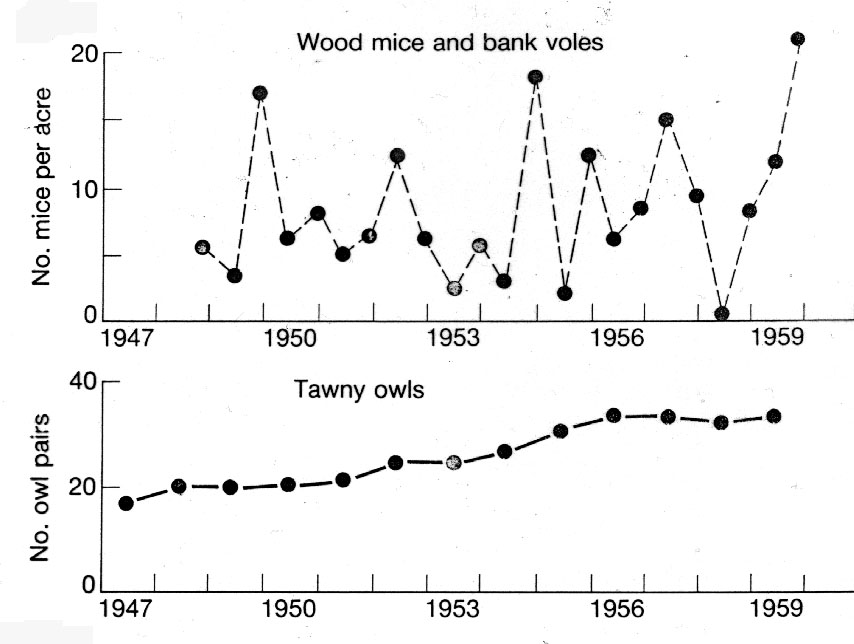
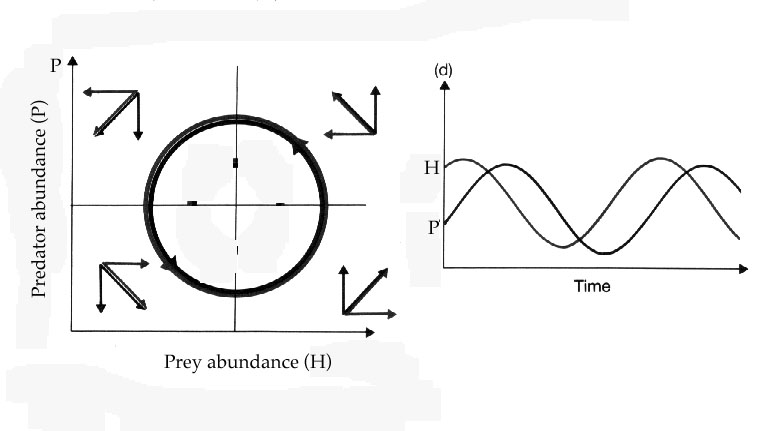
Some of this behavior is seen in the classic predator-prey case study of Lynxs and Snowshow hares. Its an excellent example of density dependent lag time in some system:

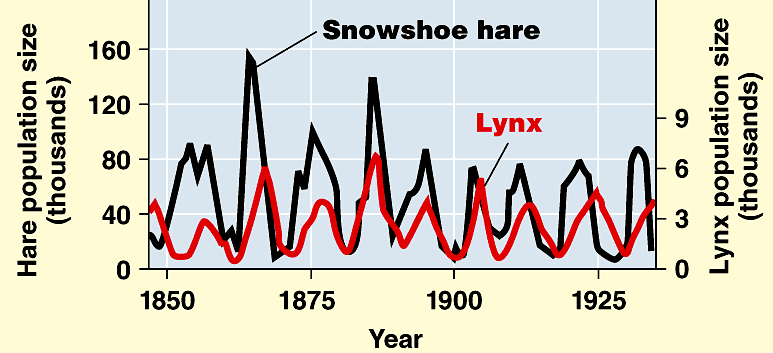
Note that this system is in quasi-equilibrium when averaged over long timescales. This is called Statistical Equilibrium .

On short time scales, however, the relative species densities are rapidly changing. Each peak or valley in this cyclical behavior is a point of unstable equilibrium and a small pertubation could drive the system completely out of control.

An additional complication is time lags or system response. In real life, this is the limiting factor for accurate modeling.

Non-linear dynamics is very difficult to accurately model because of the degree of non-linear response of the system is unknown and the relevant stress parameters are poorly understood.

But it can be effectively simulated.

Sharks and Fish Simulation

Controls/Instructions to illustrate various behaviors:
• Set size to be pretty big (67,000)
• System now should be in some kind of dynamical equilibrium
• Increase sharks a bit to input chaos
• Let the system relax

• Change fish breed to 7
• let system relax then increase sharks: density dependent lags and note that total shark population is down
• kill the system by maxing out on sharks

• hit remix
• reload the page and resize the system (slowly! to about 25000)
• let system stablize
• create pressure waves by increasing the shark starve time (7-9)
• reduce fish breed to 1 to create fractal pattern

• reload and resize to 50000
• set shark breed = 2 to produce nearly equal numbers of predator and prey in an equilibrium condition

Sometimes predator stablization can occur, if the predator can find prey over large arreas. Here is a good example from Tawny Owls in the UK

But things are that simple as outside influences can change the vectors. Dependent on what quadrant that influence operates in, the situation can be quite dramatic.

How to do simple modeling:

The simple model is that predator-prey interactios affect predator density and prey densities and then there is feedback between the two populations based on their densities.

Prey Population growth rate:

• If a prey population is left with no predators, it will (at least until it approaches carrying capacity) increase exponentially. This is seen many times when a species is released into a new habitat where predators are absent. So start with the exponential growth rate.
  dN/dt = rN N = N_oe^rt

• Introduce a predator that will slow the growth rate.
  dN/dt = rN - (ones that get eaten)

• What factors determine how many are eaten?
  • How frequently the predator and prey encouter each other which is a function of the population size of predators (P) and the population size of prey (H) so this is how predator and prey density enter into this.

  • Predator efficiency at capture, p

  • This now leads to the modified equation
    dH/dt = rH -pHP

Predator population growth rate:

• When no prey around, we can describe the decline in the predator population as mP, where the population declines exponentially at a mortality rate of m

• When prey are present, the population of predators will change like:
  dP/dt = number born - mP

• Factors relating to predation that affect the number of predators born.
  The population of predators already present, P.
  • The population of prey, H.
  • Predator efficiency at capture, p.
  • How many prey items it takes to make a new predator, or how nutritious the prey are like p, this is an efficiency (called a conversion efficiency or a below) and is a number between 0 an 1.

  • note that the product ap can be considered to tbe the reproduction rate of predators per 1 prey eaten. If a = 0.5 and p = 0.5 then ap = 0.25 meaning it would take 4 eaten prey to produce a new predator. Real world values for a and p are generally not well known.

• So the predator population is expected to change as:
  dP/dt = apHP-mP

These concepts you will actually be modeling by hand in the Zindernoodle ecosystem assignment you will get soon.

This predation model is called the Lotka Volterra model (in case you want to Google on it).

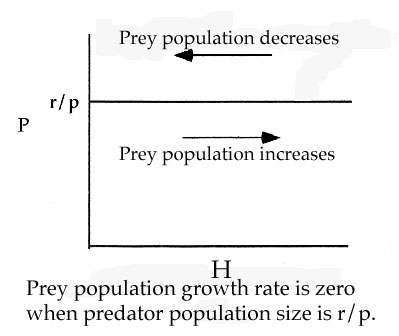
The model has two equations, one for prey populations and one for predator populations. To understand dynamics, find points when populations are in equilibrium (population growth rates of zero).

• For prey, dH/dt = 0 when rH=pHP or P=r/p

  Thus r/p is a controlling parameter

  

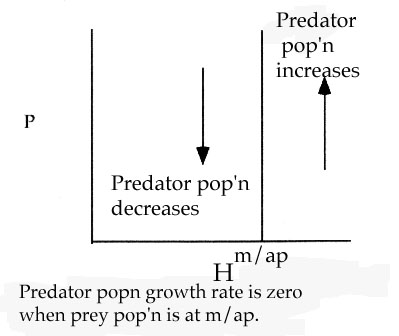
  For predators, dP/dt=0 when apHP=mp or H=m/ap

  Thus m/ap is a controlling parameter

  

When these lines of equilibrium are combined. We see that the model predicts cycling between prey and predators.

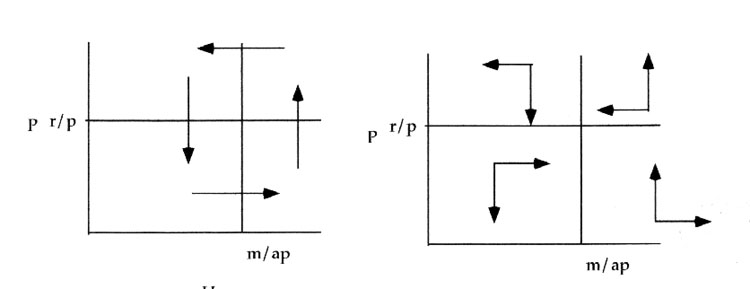
Starting from lower left quandrant and moving counter clockwise.

1. H < m/ap P falls and H grows
2. H grows until H > m/ap then P starts growing
3. When P > r/P H starts to decrease
4. As H starts to decrease, P will start to decrease as well, until H can build again

Nominal Vectors in Predator Pray relations.

Additional Resources for you to Read on the LV model:

This one

Note, what we call parameters a,m and p maybe denoted by other symbols in these other descriptions.