The Z-test

To compare two different distributions (note that the KS test has more power than this Z-test ), one makes use of a tenant of statistical theory which states that

The error in the mean is calculated by dividing the dispersion by the square root of the number of data points.

The error in the mean can be thought of as a measure of how realiable a mean value has been determined. The more samples you have, the more reliable the mean is. But, it goes as the square root of the number of samples! So if you want to improve the reliability of the mean value by a factor of 10 you would have to get 100 times more samples. This can be difficult and often your stuck with what you got. You then have to make use of it.

Ultimately the purpose of this test is to see if two distributions are significantly different from one another:

The Z-test is especially useful in the case of time series data where you might want to assess a "before and after" comparision of some system to see if there has been effect.

It is often said that you can only use the Z-test when you have a sample that your comparing against a parent population of known Mean and Standard Deviation. This is not really true - you can always use the z-test when comparing two samples.

Here is a specific example of the Z-test application:

Eugene vs Seattle Rainfall comparison over 25 years (so N = number of samples = 25):

Eugene	Seattle
mean = 51.5 inches	mean = 39.5 inches
dispersion = 8.1	dispersion = 7.0
N = 25	N = 25
error in mean = 8.1/5	error in mean = 7.0/5
error in mean = 1.6	error in mean = 1.4

The difference in mean rainfall between Seattle and Eugene is (51.5 - 39.5) = 12 inches which is 12/(sqrt(1.6^2 +1.4^2)) =6 dispersion units difference in the mean value.

Thus there is a highly significant difference in the mean annual rainfall between Eugene and Seattle.

Note this method is only an approximation. A more exact and proper way to compare two sample means will be given later.

Comparing Two Sample Means - Find the difference of the two sample means in units of sample mean errors. Difference in terms of significance is:

But for comparing two samples directly one needs to compute the Z statistic in the following manner:

In general, in more qualitative terms:

• If the difference in means between two samples is less than 2.0 dispersion units, the two samples are the same.

• If the difference in means between two samples is between 2.0 and 2.5 dispersion units, the two samples are marginally different

• If the difference in means between two samples is between 2.5 and 3.0 dispersion units, the two samples are significantly different

• If the difference in means between the two samples is more then 3.0 dispersion units, the two samples are highly signficantly different

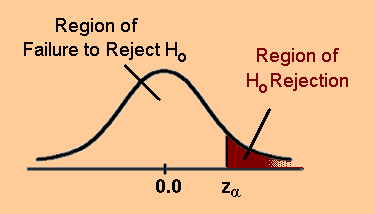
In many research areas the cricital value of Z (Z_crit) is 2.33 which represents p =0.01 (shaded area below has 1% of the total area of the probability distribution function)

Example Excel

But see the z-test in the Stastical Tools Calculator since its more straightforward to use.