A derivation of the vorticity equation from
conservation of angular momentum:
A barotropic fluid is one whose local density or density gradient
depends only on the pressure. Under those conditions, one can
write the vorticity equation as:

where ζ = relative vorticity and f = planetary vorticity; later
we will see that ζ has a shear component and what is called
a curvature component. h is the depth of our fluid and its time
rate of change represents a divergence term though this is weak
as it goes as the ln.
In more general terms, the above equation is expressed as:

An axisymmetric column of fluid rotating at a fixed
point on the Earth's surface
has two contributions to its absolute angular momentum. One is due to its motion around
the Earth's axis of rotation (orbital angular momen
tum), and the other due to its spin
around the vertical axis through its center of mass
(spin angular momentum)

If we assume the column to be only infinitesimally
wide then its rotation approximates solid body
rotation such that Ls = IΩs

So we can take the time derivative as:
D/dt(Ls) = 0 = d/dt(IΩs)
since both of these variables are function of time, then
differentiation (using the dot product rule)
leads to:
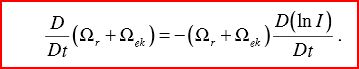

We can transform this equation into these terms

Which we can compare to our starting situation 
Are these the same?
The moment of inertia for a column is 1/2MR2 and that reduces to

where U = DR/DT = velocity of particles at radius R (assumed to be edge of the column).

And a planetary wave is then the global response of the need to conserve angular momentum in the midst of networks of smaller rotating fluids
embedded in an overall rotating atmosphere (or ocean).
Sample scale calculation:
The total vorticity is the sum of planetary vorticity + shear vorticity + curvature vorticity.
An air parcel is located at 35 degrees north. The parcel spins cyclonically (counterclock wise taking to be positive) at 15 degrees per hour due to curvature. The wind shear produces an anti-cyclonic spin. The change is wind speed over distance is 10 m/s over 300 km. What is the value of absolute vorticity at this point? For convenience we take units of vorticity as 10-5
seconds.
- Planetary vorticity = coriolis = 2Ωsin(35) = +8.37 units
- Shear vorticity: this is measured at the 500 mb level. In this case the anti-cyclonic so this is negative vorticity. In this case the shear vorticity is 10/300000 = -3.33 units
- Curvature vorticity: This basically the angular speed of 15 degrees per hour which is +7.27 units.
Absolute vorticity = 8.37 + 7.27 - 3.33 = +12.31 UNITS
Curvature vorticity is basically cyclostrophic balance and the point of this excersize was to demonstate that, at mid latitudes, the rotating of systems around some axis is a significant component of
total vorticity.
|