Blackbody radiation represents cases where all incident radiation upon a body is absorbed and then re-radiated at some characteristic black body temperature. We have previously derived this temperature for the earth but will quickly repeat
the procedure here.
F = σT4
For the Earth: (Albedo = 0.3 assumed)
Problem: A blackbody satellite (A=0) of mass = 1000 kg and radius = 1 meter orbits the Earth. It is made of material that has specific heat c = 1000 J (kg K)-1. What is the cooling rate of the satellite when it passes behind the Earth's shadow? For this case A=0 which yields Flux = 342 W per square meter and equivalent blackbody temperature of 279K. When the satellite passes into the shadow, it is no longer in radiative equilibrium as F goes to 0 and then the satellite cools via blackbody radiation, as radiated through its surfacearea, at temperature of TE  So thermal stresses on satellites are large! Atmospheric gases, in contrast, are not blackbody radiators. However, if we consider specific emissivity and absorbtivity we can approximate the atmosphere as a blackbody. Emissivity of a body is defined by the ratio of Intensity of emitted radiation to the corresponding blackbody radiation: 
Similarly, specific absorptivity, reflectivity and transmissivity are defined as: 
A guy name Kirchoff also came up with a very useful law: 
This law holds when an object is placed in a field of radation that is not isotropic or necessarily in radiative equilibrium. For gases, the law holds only when the frequency of molecular collisions is much larger than the frequency of absorption and re-emission of radiation. In essence, this is a density affect and when this condition is satisfied the system is in a state of Local Thermal Equilibrium (LTE). For our atmosphere, LTE prevailes below altitudes of about 50km. The emissivity of the earth's surface is quite complicated and varies as a function of time (due to seasonal and systematic vegetation and land use changes). Emissivity is also a function of wavelength. The figure below shows emissivity for a variery of common materials. 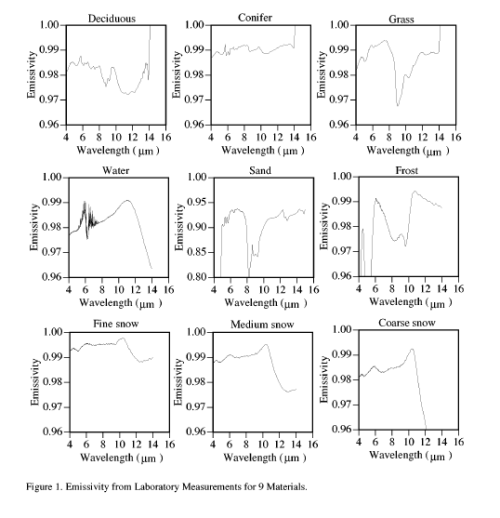  Suppose we have an object with absorptivity of 0.1 to solar radiation and emissivitiy of 0.8 to thermal infrared radiation at the top of the atmosphere. Solar constant = So = 1370 Watts per square meter (at the top of our atmosphere) The equilibrium temperature is found as follows: Energy absorbed = energy emitted = 1370 x 0.1 = 137 Energy emitted is 0.8*σ *T4 = 137; Solve for T to get 235 K. Radiative Equilbrium of the Earth: Integrating aλ and eλ produces the effective albedo and effective emissivity respectively. The energy absorbed by the Earth system is: Ea = So π Re2*(1-a) The earth heats up and re-radiates away this energy as a blackbody radiator so that the Energy emitted is Ee = 4 π Re2σTe 4 * effective emissivity (e) So that the equilibrium temperature of the earth can be specified as T4 = (1-a)*S0/4eσ or T = 255*e-.25 The observed average temperature of the Earth is 288K or 1.129 times higher than 255. To reproduce that temperature requires the effective emissivity of the earth system to be e-.25 = 1.129 or e = .62  this effectively means that the high emissivity of water is balanced by the low emissivity of rocks. In addition, the average emissivity of clouds is about 0.5 and 1/2 the earth's surface is covered by clouds.
Simple model:
so 0.5*0.5 + 0.3*0.98 + 0.2*0.85 = 0.61 ; pretty close Changes in albedo are also quite influential. For instance a change of +/- 10 % changes the equilibrium temperature of the planet to 257 and 252 K respectively. Later we will look at the rate of loss of ice coverage of the planet. For now, snow is 85% reflective and ocean water is about 7% reflective. What effect on the global albedo would occur if all the arctic sea ice were gone?
|
