The Coriolis parameter f = 2Ω sin θ can be expanded using a taylor series around θ = θ_o This expansion is useful since a real vortex will span a range of latitude and hence second order effects become important. That is , horizontal shear comes into play which is one of the things that limits the NS size of any vortex.




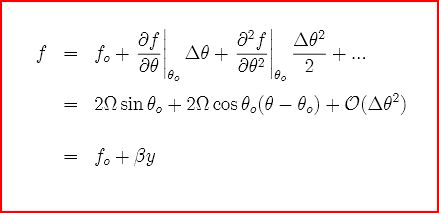
Note, this general behavior is the same in water (ocean) as it is in the atmosphere and it again is driven by the conservation rule:



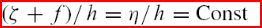
We can write down the momentum equation in one dimension where the RHS is something we have seen before in terms of cyclostrophic balance. Remember η is the absolute vorticity.

So 1D is zonal or the u component of the velocity. We then add the necessary term that accounts for latitude migration of the zonal flow because it will have a meridional (v) component:




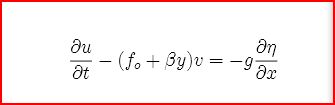
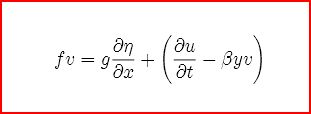
This is basically the geostrophic condition when voriticy is included and that vorticity is mostly generated by latitude migration of weather systems(the β effect). Note if v = 0 the regular cyclostrophic balance equation remains; the larger v the larger the second order effect is. Typical values for v are 12 m/s at the 500 mb height and 45 degrees latitude; this is equavilent to 1000 km in a day and this is 9 degrees in latitude. In this way latitude migration can be quite significant in the development of systems. In general, moving north will create higher wind speeds to balanced the the increase in vorticity.

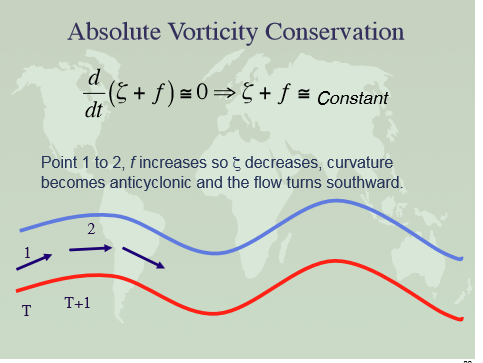
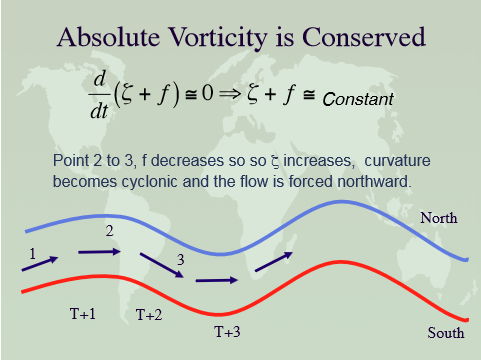
The sequence below basically shows that once a deviation from pure zonal flow happens, the response to the system is a time variable planetary wave that is the necessicary response to this deviation.



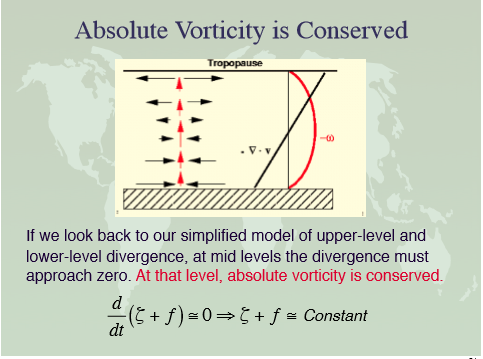
Rising air spreads out at troposphere; Divergence represents net ouflow of air; net inflow of air is convergence which is seen at lower levels of the atmosphere.













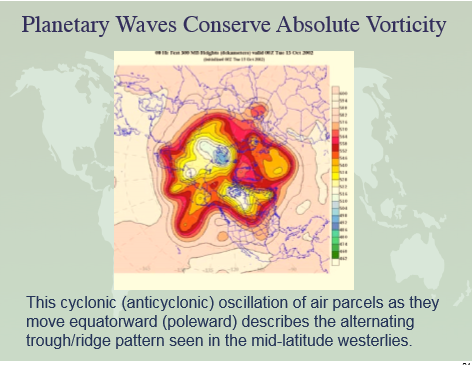
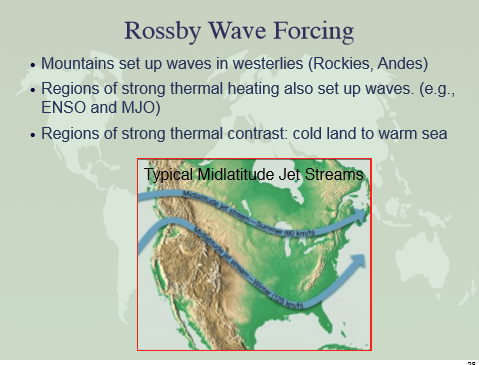
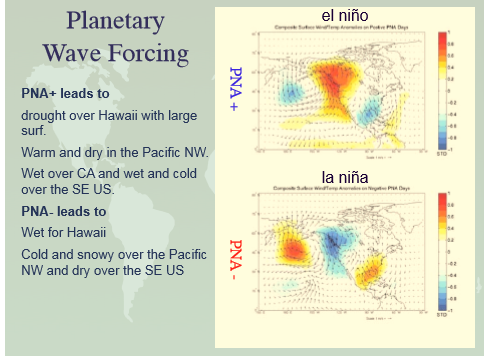
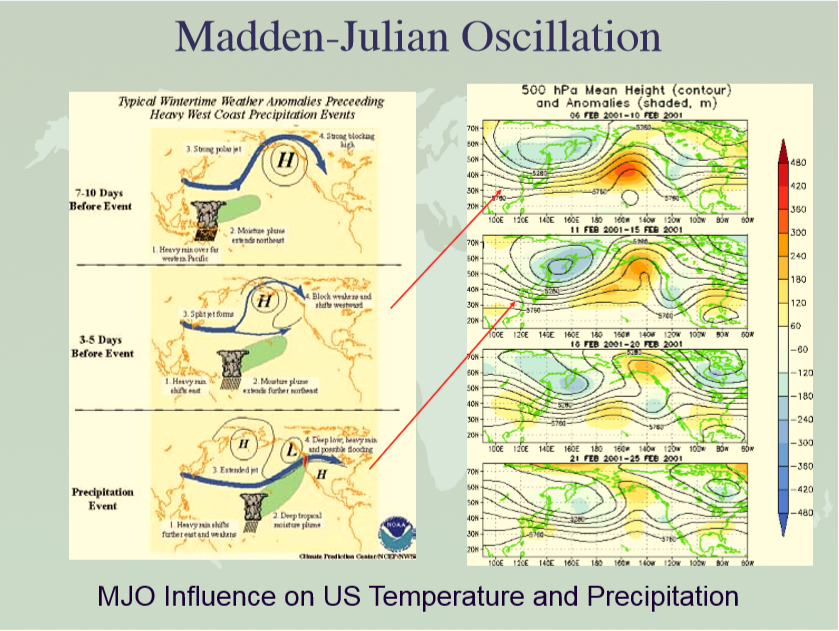
Climate, Weather and Rossby Waves:

Persistence of blocking patterns:
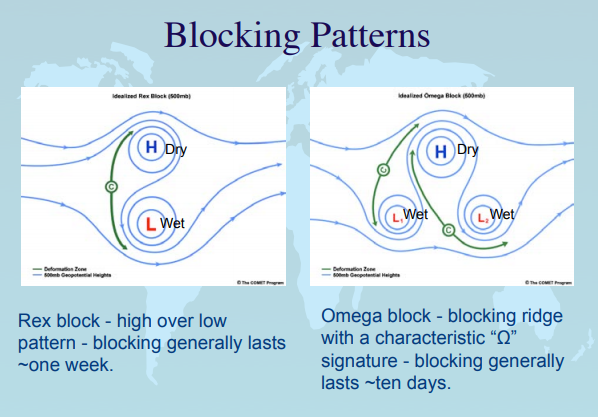
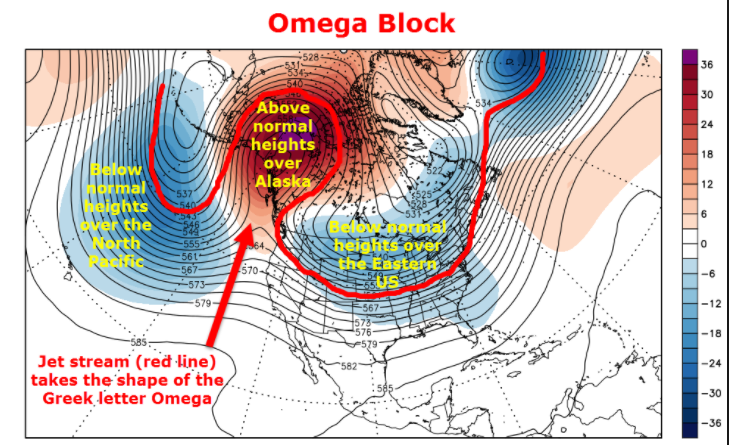