Tornadoes come in a variety of shapes and sizes - with varying residence times on the ground. Nowadays, large tornadoes are observed to spend 20-25 minutes as a single feature on the ground.



To first order, torandoes can be described in terms of Cyclostrophic balance, pressure gradients and the induced vertical pressure gradient as a consequence of cylinder rotation:



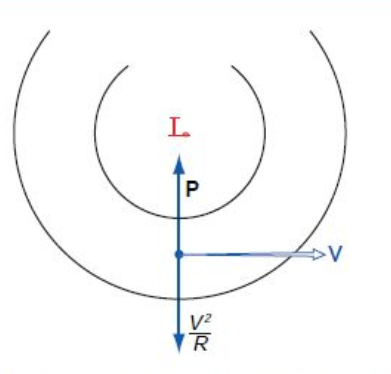
Example: Air in solid body rotation has a radius of 2km and a period of 15 minutes. What is the amplitude of the dynamically-induced radial pressure gradient? (V²/R is a "force").

Under cyclostrophic balance,





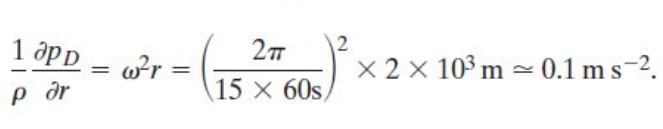
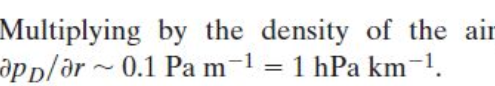
The intensity of the dynamically induced pressure gradient goes as the square of the rotation velocity, which is much lower at lower alititudes (primarly because of friction) than at higher altitudes:



What is the upward acceleration due to this induced pressure pertubation from to ground to altitude 1 km?



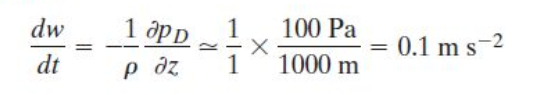
Over an interval of 1 minute, this imparts a vertical velocity of 6 m/s to the air beneath the updraft and that allows the system to maintain itself as its rotational velocity strengthens.

Also, how large of temperature pertubation is needed to impart a hydrostatically balanced vertical acceleration of 0.1?

Recall from before when we discussed buoyancy induced vertical motions.

To maintain cyclostrophic balance (at all vertical levels) a rather large pressure difference between the tornado center and the environment is required. This can be seen in this numerical example:

In general the radial profile of tangential wind speeds as well as the vertical velocity in tornadoes are not well known from measurements. So we need to make a simple model.

• Use a velocity of 100 m/s for tangential
• density of the air is 1.25
• Ingore the variation of air density with pressure
  
  
  
  ρv² is a pressure (dimensional analysis) - it represents flow induced pressure that occurs through mass (density) transport in the fluid.
  
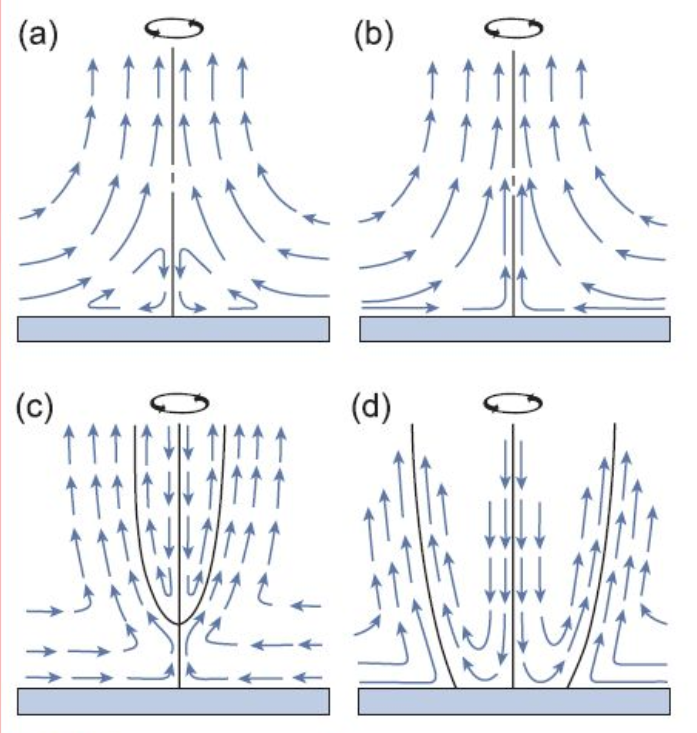
  Vorticity concentration and conservation act as stretch mechanisms that create the tornado collimated funnel.
  
  
  
  Now the vertical stretching occurs with within the lowest 1-2 km above the ground (i.e. the funnel doesn't rise higher than 2 km. In this regime, we again assume the density is constant. In this case the time evolution of the vortcity is
  
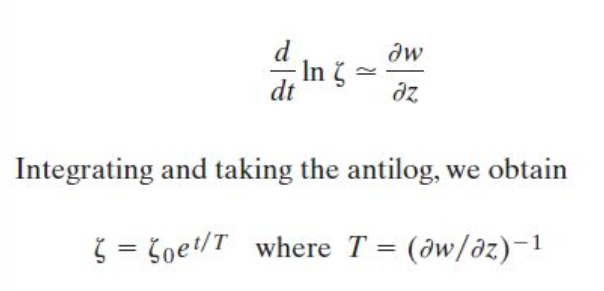
  Remember, dw/dz is the thing that induces the radial pressure gradient allowing the system to spin up.
  
  Limited data suggest that w is zero at the ground at 3 m/s at 1 km.
  
  so dw/dz = .003 so e-folding time = 300 seconds (which is less than the duration time of the tornado so voriticy can and is enhanced!
  
  So given an ambient vorticiy of .01 and a 5 min e-folding time, how long would it take to produce tornado (assumed to be axially symmetric) with v = 100 m/s and a radius of r = 200m? Again we assume solid body rotation inside this radius.
  
  
  
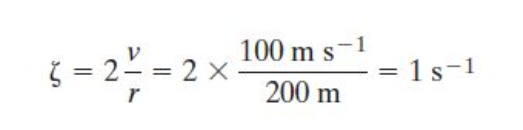
  Now we have to increase vorticity by a factor of 100
  
  
  
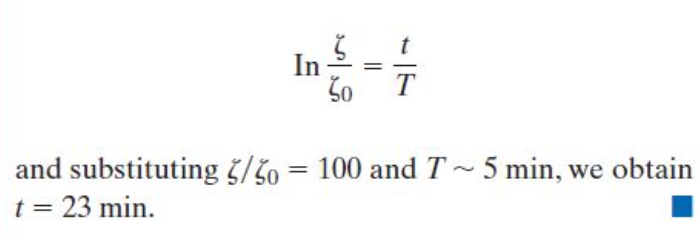
  In good agreement with real world observations.
  
  But real tornadoes are not in solid body rotation and develop local regions of extremely high vorticity which will break down into multiple vortices. This is also the reason that tornadoes can not get arbitrarily high as the induced extreme vorticity will break the fluid apart.
  
  Flow development: