Z-test Compared to Salmon Count Data

Let's now apply the Z-test to some real data for illustrative and practice purposes. The data shown below is over a 44 year period (1951-1995) for salmon counts at the McNary Dam. (We will later in this course be dealing with up-to-date salmon count data. This is just an example of how to apply the Z-test.)

The actual salmon count data shown as a histogram of the number of years where the salmon counts landed in the indicated bins. (Bins are 50,000 salmon counts wide.)

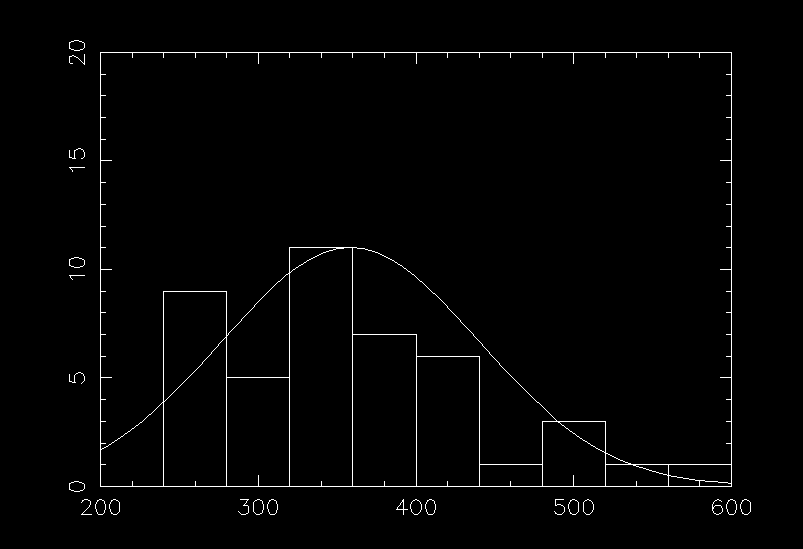This distribution, defined by 44 points, has a mean of 358,000 salmon with a dispersion of 82,000 salmon. The error in the mean is 12,000 (82000/(square root of 44))

Points to note about the distribution:

1. The dispersion is fairly large. Is this intrinsic to the population or a reflection of measuring errors because salmon counting is difficult and unreliable?
   
   
2. There seems to be a hard lower limit in the data of around 225,000 salmon.
   
   
3. There is a tail towards very high salmon counts (> 500,000 salmon). Tails like this have a significant impact on the mean value and might represent some kind of anomaly in the data.
   
   
4. Overall, the distribution is not real well fit by a bell curve. However, the median value of 340,000 is similar to the mean, so we can use our principles of dispersion to calculate significant differences.

There has been some speculation and data that suggest there has been a decline of salmon recently in the Columbia River System. What do these data say?

Here is the distribution of the data with the last 5 years subtracted out, so there are 39 years worth of data:

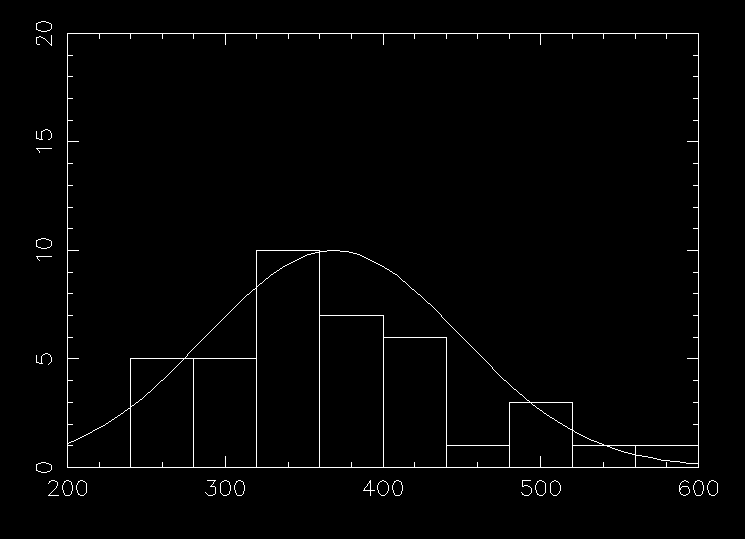This distribution, defined by 39 points, has a mean of 368,000 salmon with a dispersion of 81,000 salmon and a mean error of 13,000.

Note: The dispersion for the 39 year sample and the 44 year sample are similar this indicates that we have enough data to accurately determine the dispersion.

Over the last 5 years, the data are defined by an average of 278,000 salmon with a dispersion of 33,000 and a mean error of 15,000 = (33,000/(sqrt of 5)). Does this data show a significant decline of salmon?

Well, we would plug our means and mean errors into the formula for the Z-test, but you can just plug the numbers into The Z-test tool. (Note: in this particular tool, you can enter the straight standard deviation and the number of data points - the tool automatically calculates the error in the mean from that.)

You should find a Z-statistic of 4.6 indicating high significance.

Hence, in 1996, you could have used statistics to definitively show a strong decline in the salmon population. However, this would require that the 44 year sample is an accurate reflection of the general phenomena and, as it will turn out, salmon counts/abundance are highly cyclical in nature and that 44 year snapshot of the population from one dam is not representative.

(Note that it will turn out that salmon counts will start to strongly rise in the late 90's.)