Solar Energy

The Basics of Solar Energy

The national solar resource has considerably variation in both place and time. Hence strategic investment is important.

The sun Always there; lots of energy.

How many photons (energy) reach the surface of the Earth on average?

The energy balance in the atmosphere is qualitatively shown here:

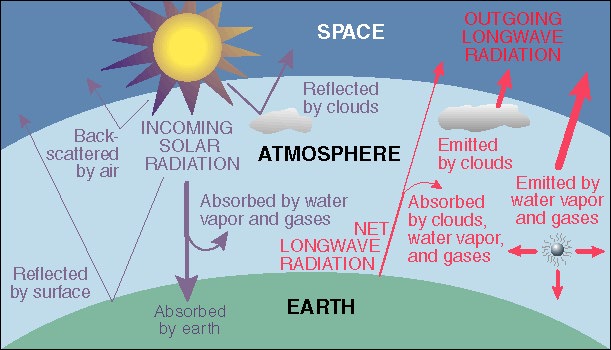
The main components in this diagram are the following:

Short wavelength (optical wavelengths) radiation from the Sun reaches the top of the atmosphere.
Clouds reflect 17% back into space. If the Earth gets more cloudy, as some climate models predict, more radiation will be reflected back and less will reach the surface.
8% is backwards by air molecules.
6% is actually directly reflected off the surface of the Earth (on average) back into space.
So the total reflectivity of the Earth is 31%. This is technically known as an albedo. Note that during Ice Ages, the albedo of the Earth increases as more of its surface is reflective. This makes it difficult for the Earth to warm back up - yet, it's a clever system.

What happens to the 69% of the incoming radiation that doesn't get reflected back:

19% gets absorbed directly by dust, ozone, and water vapor in the upper atmosphere. This region is called the stratosphere, and it's heated by this absorbed radiation. Loss of stratospheric ozone is causing the stratosphere to cool with time this has caused some to use stratospheric cooling as an argument against the occurrence of global warming. The two are not connected at all.
4% gets absorbed by clouds located in the troposphere. This is the lower part of the Earth's atmosphere where weather happens. This part of the equilibrium cycle is being changed as the troposphere, particularly at tropical latitudes, is getting cloudier.
The remaining 47% of the sunlight that is incident on top of the Earth's atmosphere reaches the surface. This is not a real significant energy loss Therefore it makes absolutely no sense to put solar panels in orbit and then "beam" the energy back to the surface.

Averaged over the entire, Earth = 164 watts per square meter over a 24 hour day so the entire planet receives about 85,000 terrawatts of power our current worldwide power use is about 14 TW (of which 3.5 are required for the US alone). Since the Sun gives us 84,000, and we only need 15 Is this a solution?

In principle, we would need 14 terrawatts (= 14 x 10¹² watts) divided by 164 watts per square meter = 10¹¹ square meters of collecting area.

But since our efficiency will only be about 10% (see more below), then we need 10¹² square meters which is equal to one million square kilometers.

Now, suppose we could construct an equatorial grid with one station per time zone. Then we would need 24 installations each of size 200 x 200 km. This is formidable!

and remember, little of the world current runs on
renewable energy sources:

There is a large amount of infrastructure (e.g. cost) required to convert from potential to deliverable energy.

8 hour summer day, 40 degree latitude

600 watts per sq. meter

So over this 8 hour day one receives:

8 hours x 600 watts per sq. m = 4800 watt-hours per sq. m which equals 4.8 kilowatt hours per sq. m.
This is equivalent to 0.13 gallons of gasoline.
For 1000 square feet of horizontal area (typical roof area), this is equivalent to 12 gallons of gas or about 450 KWH.

But to go from energy received to energy generated requires conversion of solar energy into other forms (heat, electricity) at some reduced level of efficiency.

We will talk more about PV cells in detail later. For now the only point to retain is that they are quite low in efficiency!

Collection of Solar Energy

The amount of captured solar energy depends critically on orientation of collector with respect to the angle of the sun.

Under optimum conditions, one can achieve fluxes as high as 2000 watts per sq. meter.
In the winter, for a location at 40 degrees latitude, the sun is lower in the sky and the average flux received is about 300 watts per sq. meter.

A typical household winter energy use, with electrical heating, is around 2000-3000 KWHs per month or roughly 70-100 KWH per day.

Assume our roof top area is 100 square meters (about 1100 square feet).

In the winter on a sunny day at this latitude (40^o) the roof will receive about 6 hours of illumination.

So the incident solar energy over this 6 hour period is:

300 watts per square meter x 100 square meters x 6 hours

= 180 KWH (per day) more than you need.

But remember the efficiency problem. We have to build a device to convert incident solar power into deliverable power. For now, again we don't care what the device is, only that is efficiency lies somewhere in the range below:

5% efficiency 9 KWH per day
10% efficiency 18 KWH per day
20% efficiency 36 KWH per day

At best, this represents 1/3 of the typical daily winter energy usage, and it assumes the sun shines on the rooftop for 6 hours that day.

With sensible energy conservation and insulation and south facing windows, it's possible to lower your daily use of energy by about a factor of 2. In this case, if solar shingles become 20% efficient, then they can provide 50-75 % of your energy needs.

These considerations suggest that solar PV rooftops (e.g., solar shingles) are likely a generically good idea.

What about the prospect of "solar farms" and remote power delivery?

The relative inefficiency can be compensated for with collecting area.

Examples

A site in Eastern Oregon receives 1200 watts per square meter of solar radiation in July. Assume that the solar panels are 10% efficient and that they are illuminated for 10 hours.

How many square meters would be required to power Eugene at 300 megawatts?

Each square meter gives you 1200 x.1 = 120 watts

Remember, we want 300,000,000 Watts, not just 120.

There are one million square meters in one square km.

So, each square km gives your 120 x 1,000,000 = 120 MW.

Therefore 2.5 square kilometers would be enough to power Eugene

Ten square kilometers would give you about 1200 MW keep this as a figure of merit reference under optimum conditions.

Now, of course, you wouldn't have continuous coverage. The individual collectors would have to be spaced out.

And so, in practice, the actual land use is about twice as great per MW generated. In addition, 1200 watts per square meter in July is about 2.5 times larger than the annual average. These considerations then produce the following rubric:

10,000 Megawatts of Average Annual Solar Power (when the sun is shining) requires 500 square kilometers of collecting area (at 10% efficiency).

This is why any gain in efficiency is incredibly important.