
How fast will Resource X be depleted?
Well suppose we have the following situation:
 Dear Congressperson, when
will resource X run out.
Dear Congressperson, when
will resource X run out.
Congressperson says "oh don't worry, Resource X will be around for 100 years"
Really .... don't we use resources like rabbits?

70/n years; n =% growth rate
Its important to recognize that even in the slow growth period, the use of the resource is exponential. If you fail to realize that, you will run out of the resource pretty fast.
The correct equation for calculating the exponential exhaustion timescale of any resource (should be required knowledge for any one elected to congress):
where k = growth rate
R = total resource available
ro = initial consumption rate
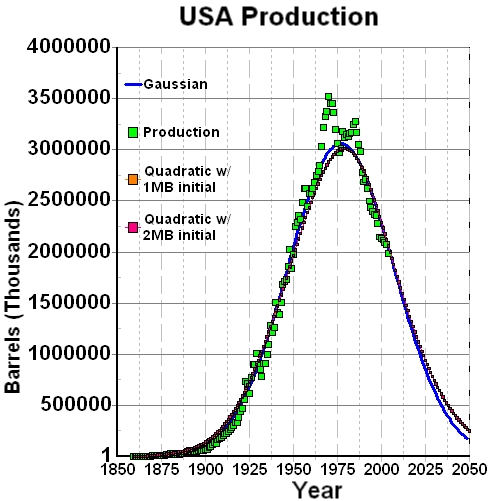 Let's start out with the curve for US Oil production. Note that peak production occurs on a timescale of
1/2 of Te as the production curve is assumed to be symmetric. When resources reach peak production, prices tend to
go up which can then serve to lower consumption and extend the exhaustion timescale.
Let's start out with the curve for US Oil production. Note that peak production occurs on a timescale of
1/2 of Te as the production curve is assumed to be symmetric. When resources reach peak production, prices tend to
go up which can then serve to lower consumption and extend the exhaustion timescale.
In 1956, M. King Hubbert published an ignored paper based on this methodology as applied to US Oil production.
Other Examples to do in the Excel Template. Following are best estimates for 2010:
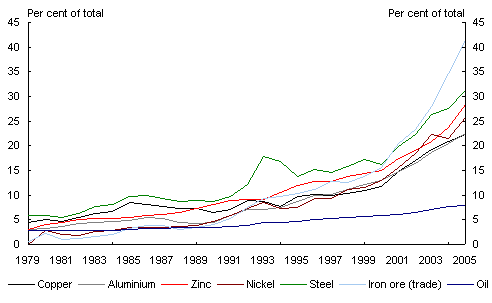
 production of steel
R/r = 30 Market Reaction!
production of steel
R/r = 30 Market Reaction!
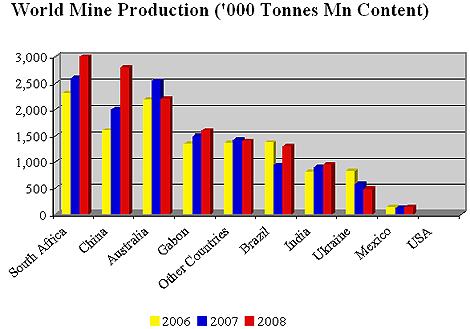
Be very aware of this - a little reported fact in US Media Rare Earth Minerals are relevant to most aspects of a scaleable green economy!
So on the surface, application of Hubbert's methodology strongly suggests that the world is going to
experience peak production on a variety of mineral and other
resources. Various economic corrections will then occur and prices will daramatically rise as
a result of real, global, scarcity.
Back to Congress:
The basic problem is that we substitute Disney's First Law for this arithmatic reality of resource depletion.