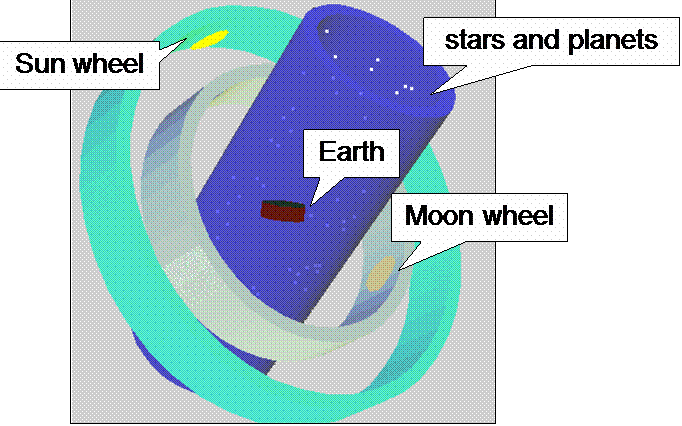
The Earth Centered Models:
Anaximander: The precursor to the Cystalline
spheres of the Aristotle - The Earth as a Cylinder
floating in the center of the Universe.
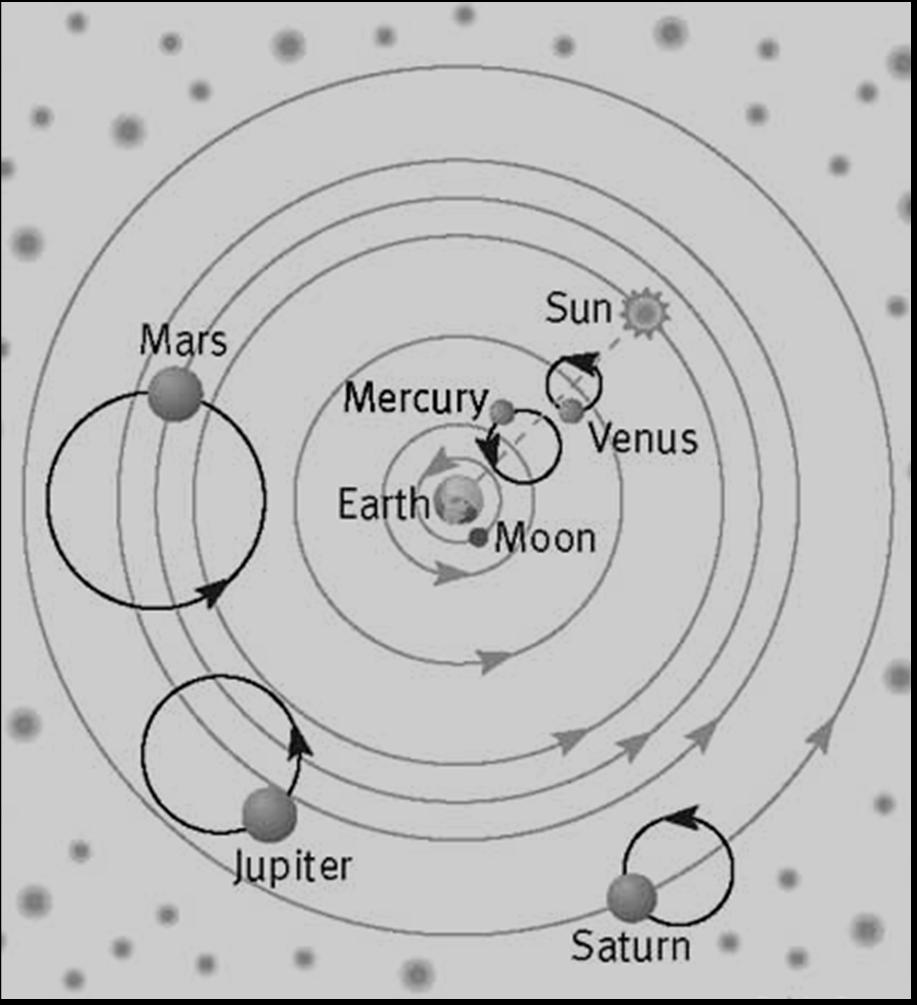
Ptolemaic System with Epicycles - Note that the Earth and Sun are "joined" to constrain Mercury and Venus
Aristarchus (310 - 230 B.C.)

Aristarchus developed methods to measure the relative sizes and distances of the
Sun and the Moon. Even though his measurements are wrong, he does correctly conclude
that the Sun must be much bigger than the moon and that the Earth and the moon are
roughly the same size  therefore the Earth
must go around the sun, the larger of the three objects.
therefore the Earth
must go around the sun, the larger of the three objects.
Aristarchus is a Phythagorean so his whole life revolves around what can you do
with right angles and 1+2+3+4 = 10 = perfect numbers, etc, etc.
His method consists of three parts:
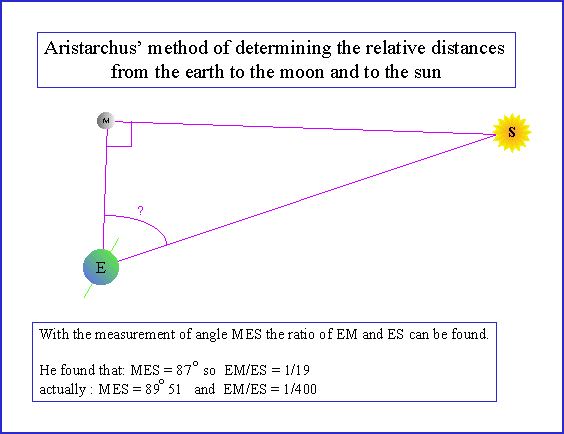 When the Moon is exactly half full, the angle E-M-S must be
exactly 90 degrees (this requires an understanding of the proper reason
for lunar phases ). Therefore, a measurement of the angle M-E-S when the Moon
is half full will give the ratio of the Earth-Moon distance to the Earth-Sun distance.
Difficulties include a) hard to determine exact center lines to the moon and especially the Sun,
b) refraction at sunset, and c) hard to know when the moon is exactly at 1/2 phase. So he gets
19 to 1 as the ES/EM ratio.
When the Moon is exactly half full, the angle E-M-S must be
exactly 90 degrees (this requires an understanding of the proper reason
for lunar phases ). Therefore, a measurement of the angle M-E-S when the Moon
is half full will give the ratio of the Earth-Moon distance to the Earth-Sun distance.
Difficulties include a) hard to determine exact center lines to the moon and especially the Sun,
b) refraction at sunset, and c) hard to know when the moon is exactly at 1/2 phase. So he gets
19 to 1 as the ES/EM ratio.
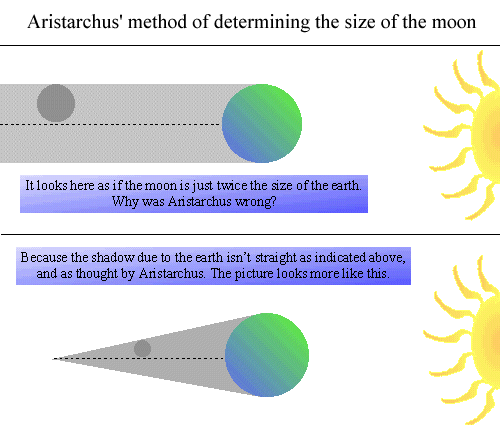 During a lunar eclipse, he measured the duration
of time between the moment when the edge of the Moon first became eclisped and
the moment when the Moon was first totally obscured. He also measured the duration of totality.
Because he found the two times to be the same, he concluded that the width of the
Earth's shadow at the distance where the Moon crosses it must be twice the diameter of the Moon.
Therefore, the Moon must be 1/2 the size of the Earth
During a lunar eclipse, he measured the duration
of time between the moment when the edge of the Moon first became eclisped and
the moment when the Moon was first totally obscured. He also measured the duration of totality.
Because he found the two times to be the same, he concluded that the width of the
Earth's shadow at the distance where the Moon crosses it must be twice the diameter of the Moon.
Therefore, the Moon must be 1/2 the size of the Earth
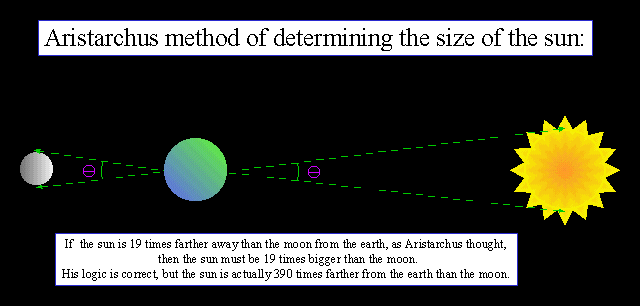 Aristarchus also reasoned that since the Sun
and the Moon have the same angular size (which is why there can be a total eclipse of the
Sun), but the Sun is 19 times further (or so he thought),
then the Sun must be 19 times bigger than the Moon.
Aristarchus also reasoned that since the Sun
and the Moon have the same angular size (which is why there can be a total eclipse of the
Sun), but the Sun is 19 times further (or so he thought),
then the Sun must be 19 times bigger than the Moon.



 therefore the Earth
must go around the sun, the larger of the three objects.
therefore the Earth
must go around the sun, the larger of the three objects.
 When the Moon is exactly half full, the angle E-M-S must be
exactly 90 degrees (this requires an understanding of the proper reason
for lunar phases ). Therefore, a measurement of the angle M-E-S when the Moon
is half full will give the ratio of the Earth-Moon distance to the Earth-Sun distance.
Difficulties include a) hard to determine exact center lines to the moon and especially the Sun,
b) refraction at sunset, and c) hard to know when the moon is exactly at 1/2 phase. So he gets
19 to 1 as the ES/EM ratio.
When the Moon is exactly half full, the angle E-M-S must be
exactly 90 degrees (this requires an understanding of the proper reason
for lunar phases ). Therefore, a measurement of the angle M-E-S when the Moon
is half full will give the ratio of the Earth-Moon distance to the Earth-Sun distance.
Difficulties include a) hard to determine exact center lines to the moon and especially the Sun,
b) refraction at sunset, and c) hard to know when the moon is exactly at 1/2 phase. So he gets
19 to 1 as the ES/EM ratio.
 During a lunar eclipse, he measured the duration
of time between the moment when the edge of the Moon first became eclisped and
the moment when the Moon was first totally obscured. He also measured the duration of totality.
Because he found the two times to be the same, he concluded that the width of the
Earth's shadow at the distance where the Moon crosses it must be twice the diameter of the Moon.
Therefore, the Moon must be 1/2 the size of the Earth
During a lunar eclipse, he measured the duration
of time between the moment when the edge of the Moon first became eclisped and
the moment when the Moon was first totally obscured. He also measured the duration of totality.
Because he found the two times to be the same, he concluded that the width of the
Earth's shadow at the distance where the Moon crosses it must be twice the diameter of the Moon.
Therefore, the Moon must be 1/2 the size of the Earth Aristarchus also reasoned that since the Sun
and the Moon have the same angular size (which is why there can be a total eclipse of the
Sun), but the Sun is 19 times further (or so he thought),
then the Sun must be 19 times bigger than the Moon.
Aristarchus also reasoned that since the Sun
and the Moon have the same angular size (which is why there can be a total eclipse of the
Sun), but the Sun is 19 times further (or so he thought),
then the Sun must be 19 times bigger than the Moon.