In principle, the formula that we have been using would allow the female adults to live forever (and reproduce forever).

This is obviously unphysical and so one needs to introduce a correction factor, w , which represents the maximum reproductive age of a species (something that's actually hard to measure).

The corrected expression looks even more horrible than the first one.

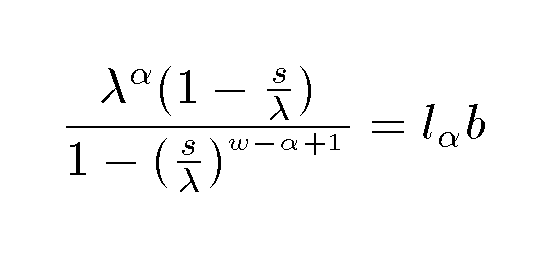
Before we collectively freak out, let's examine this new equation to see if it makes sense in some physical limits.

In the first case, let w approach infinity. In that case, s/λ is less than 1 and (s/λ)^w would be 0 and we recover our initial equation.

In the case where w=α (i.e. the female dies when they reach reproductive age) we would have the condition

λ^α = l_αb

Which is exactly what you get if you formally make s =0 in the previous equation. And we just stated this condition: when the female reaches their reproductive age, α, they die and hence have no adult female survival probability.

As you will determine in your exercise, and as we will see below, the addition of w makes a very big difference.

We will use the example from before where:

• α = 4 years
• s = 0.90
• s_o = 0.15
• s₁ = 0.70
• b = 0.25

So we would have on the right hand side (RHS) of the equation:

l _α = 0.90 * 0.15 * 0.70 = .095

l _α b = .095 *.25 = 0.0236

therefore,

λ⁴(1 - .90/λ) = .024 ; solved with λ =.93

Lets take the case of w = 15 years for the previous data set. We then have the same right hand side as before (0.024) and the same numerator (λ⁴(1 - .90/λ) as before:

But this is now corrected by the term in the denominator which is

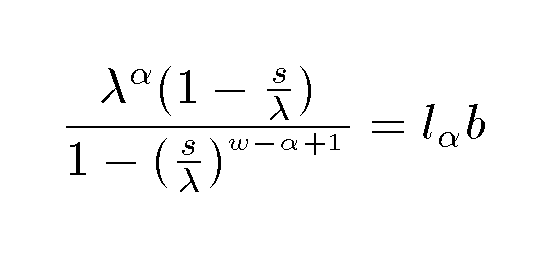
(1 - (.90/λ))¹² ; 12 = 15-4+1

Putting this into the iterative spead sheet and incrementing λ until we get an approximate solution yields λ = 0.83 or a fractional decrease in the population of 17% per year - this is a lot bigger than the previous decrease of 7% a year and we get a population crash time of 48 years, instead of 123 years.

So, w makes a big damn difference!