Part 1:

The Spooky Tooky is a large owl-like creature that tends to inhabit and mate in Old Growth Forest. The Spooky Tooky was once abundant in the wilderness but with the coming of the chain saw , the Spooky Tooky population is starting to dwindle. The Spooky Tooky population is important to the overall health of the ecosystem since they prey on the spineless manga toad that likes to suck the sap out of old growth trees, thus causing them to fall over, dead.

In addition, the Spooky Tooky can perform barrel rolls and loop to loop on command for the the entertainment of tourists visiting our National Forests. Thus, there is a keen need to develop effective policy to preserve the Spooky Tooky.

At last count, there were 12000 individual Spooky Tookies known. They are known to be long lived creatures and Sparky, the best known of all Spooky Tookies, is at least 60 years old (a.k.a. Sr. Tooky).

The Spooky Tooky, like most creatures in the forest, mate and produce offspring. Preservation of the Spooky Tooky then requires a habitat which a) lets them mate b) lets them have female offspring and c) lets the female offspring have a reasonable probability of living long enough to mate and have more female offspring. The Spooky Tooky long ago discovered the Viagra tree and even old Sparky can still produce offspring, provided he can find a mate.

For a species like the Spooky Tooky, it can be shown that the geometric growth rate of the population can be approximated by the following equation:

The terms in the above equation are the following:

• λ = the growth rate; values of λ less than 1 lead to population crashes.

• α = the age at which the species starts breeding

• s = the adult annual survival probability

• b = adult average female fecundity - fecundity means the power of a species to multiply rapidly or its capacity to form reproductive elements. It is one measure of fitness. In the case of the Spooky Tooky b means the average reproductive rate of female offspring per adult female in the overall population per year.

• l_α represents the probability that a new born will survive to age α (the breeding age).
  note that l_α in turn = s_o * s₁ * s where s_o = survival probability at birth and in fledgling stage of life, s₁ = sub-adult annual survival probability, and s is as given above.

Given a value of λ, we can then estimate the characteristic timescale of the population crash as

where N is the number of known individuals in the population (12000) in this case.

Below are three sets of data that have observationally determined the necessary parameters.

The three data sets come from the following agencies:

• A Government agency in charge of managing the old growth trees. They insist that the Spooky Tooky habitat is in good shape and the population is sustainabile.

• University Biologists who have a grant from the Government agency that has declared the species sustainable

• The personally funded study of Sunshine Moonbeam, again, President of the Sierra Club, whose position is quite firm that the majestic Spooky shall be no more, pretty soon, at the present rate of development.

Your first task is to derive estimates of λ and τ (the population crash time) from each of these data sets.

Data Set 1 (from a Government Agency):

• α = 3 years
• s = 0.95
• s_o = 0.15
• s₁ = 0.72
• b = 0.24

Data Set 2 (from University Biologists)

• α = 4 years
• s = 0.85
• s_o = 0.10
• s₁ = 0.50
• b = 0.28

• α = 2 years
• s = 0.65
• s_o = 0.05
• s₁ = 0.35
• b = 0.20

When a group of university biologists went to the Spooky Tooky policy hearings, they were met by an angry mob of legislators that a) complained that university professors are overpaid and b) that they had done their study wrong by implicitly assuming that the Spooky Tooky, if they survive as an adult, lives for a very long time. Even though the biologists had Sr. Tooky with them to prove their point, the legislators refused to believe that ol Sparky was really 60 years old.

The legislators then whipped out a formula produced at the Institute for Scientists that Whip out Formulas in which a new parameter w is now introduced. According to the Institute Scientists, the w parameter represents the maximum age for survival and reproduction.

This whipped out formula is even more horrible that the first one:

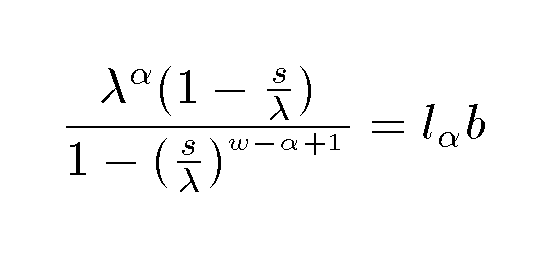
The republican legislators insist that w = 15 years while the democrats insist that w = 10 years. In turn, the StarDust party of SunShine MoonBeam hangs on to the mystical belief that w = 6 years and that Sr. Spooky merely looks old for his age.

The University Biologists are all democrats. Using these preferred values of w your third task is to correct the previous results that each study derived, for this finite lifetime effect, and to re-determine the values for λ and τ. Which study, as determined by the difference in crash time ratios, seems to have the most sensitivitity to the assumed value of w? In particular, how does the StarDust party's value help to sell their agenda?

Since the effects of the w parameter is quite confusing, your 4th task is to produce a graph that shows the relation between λ and w for each of the three data sets by varying w over a relatively large range.

Part 2:

Application to Humans:

1. Plug in values of the various parameters to see what combination of parameters (e.g. α, w, s,s_o,s₁, b ) to see which combination gives us a value for λ between 1.01 and 1.02, which is approximately the growth rate of the world over the last 100 years.

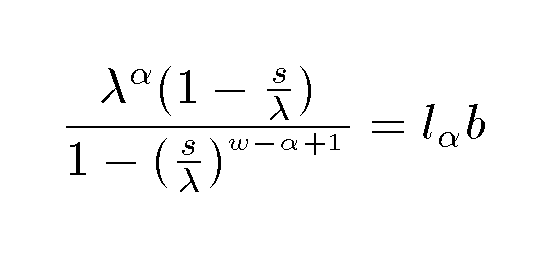
   So in the spread sheet first set λ to something between 1.01 and 1.02 and then adjust the other parameters the difference between the LHS and the RHS is close to zero. Note that you should be able to get within less than 0.001 for this difference.

2. Now let's try and see if its possible, via some combination of parameters, to get λ = 1.005 (very slow exponential growth). (again less than 0.001 diff)

3. Finally, try to find a solution that produces λ = 0.99. (again less than 0.001 diff) What are the implications of this solution?