Density Dependent Consumption

Premise: the rate of prey consumption by a predator rises as prey density increases

But, what is the functional form of this rise and what are the limits? For instance, is it linear (Y = ax +b) or might there be other issues that complicate this simple expectation?

What might some of the variables be to consider:

Let's think about predators - what do they do?

• Look for and locate potential prey to consume - We call this time the "search time".
  
  
• Spend time (which we call "handling time") chasing, catching, killing, eating and digesting.

This handling time concept now limits a predators consumption rate, espcially if the handling time is large. Lions are a good example of this.

The total predator time (take this as the lifetime of the predator) is

T = T_search + T_handling

Now let's specify H_a as the amount of prey captured by the predator during time T (this would be an integer number and is essentially the total amount of prey consumed over the lifetime of the predator). The little a refers to "attack".

Since handling time should be directly proportional to prey capture rate we have:

T_handling = H_aT_h

where T_h is the time spent on handling of 1 prey.

What is the capture strategy of a predator? Mostly random. A predator hunts around some area over some time interval and so there is a "search rate" parameter ( eagles ) which we will call α which has units of area/time (e.g. meters²/seconds) - also we assume that a predator only eats one prey at a time.

After searching for some time, T_search, a predator has covered an area of:

αT_search(meters²/seconds x seconds = meters²)

and has captured:

αT_search * H

prey, where H is the prey density per unit area (N/area).

So,

by definition H_a =αT_search*H

or

αT_search = H_a/H

isolating T_search leads to

T_search = H_a/α H

Now one evaluates the total time budget over the predator lifetime spend in the search and handling phases (this is all that a predator does).

T = T_search + T_handling = H_a/α H + H_aT_h

We are interested in expressing H_a as a function of H (the prey density - hence density dependent consumption ) and T.

Again, H_a is the amount of prey captured by the predator during time T.

1. factor out H_a T = H_a*(T_h + 1/αH)

2. rewrite (T_h + 1/αH) as (αHT_h/αH + 1/αH)
   
   or (αHT_h +1)/αH

3. we now have T = H_a(αHT_h +1)/αH

4. and then H_a = αHT / (1 + αHT_h) (doesn't mean squat until you plot it)

Well that is a bunch of algebra which is mostly useless; insight into this forumalism comes from graphing the function and thinking about.

In brief, this function is non-linear and has an asymptotic form. This means that for low values of H (the prey density) H_a will grow linearly, at a slope that approximates α (the search rate parameter). But that linear coupling does not remain as higher values of H will create a negative feedback and creates a maximum value of H_a = T/T_h

for the asymptotic case where aHT_h >> 1 then H_a = αHT / (1 + αHT_h) goes to

H_a = αHT /αHT_h = T/T_h

This equation -- H_a = αHT / (1 + αHT_h) -- has a functional form that looks like this:

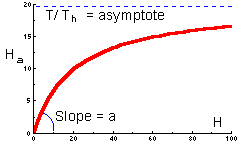
How does one interpret this?

• There is a specific amount of handling time (T_h) associated with each prey item eaten or attacked that is invariant of the density of the prey (H). This is exactly what creates the feedback. If your the lion, who has just eaten a deer, then your going to lie around for hours/days before finding the next deer.

• Thus, while prey items are easier to find as their density increases, handling time per prey item is the same, and the maximum number of prey items eaten or attacked is determined by the ratio of total available time to handling time (T/T_h).

• The feedback is that as prey density increases (therefore decreasing search time), the proportion of total Time spent in the handling phase increases. (T = lifetime of predator = constant = T_search + T_handling)

  
  
  

• When all available time is spent handling prey, you can only process/attack prey at a constant rate and hence the number of attacked prey levels out (reaches a plateau).

• Sharks behave like this to some extent which is why there can be plenty of food swimming around them

The entire point of introducing this methodoloy is to introduce the concept of system feedbacks which limit rates and ultimately bounds system behavior. This methodology for feedback can also apply to climate change modeling that we are getting to.