Solar System Composition












But note that 99.85% of the mass of the solar system is in the Sun. Below
is a scaled drawing of all the diameters of the planets relative to the
Sun.
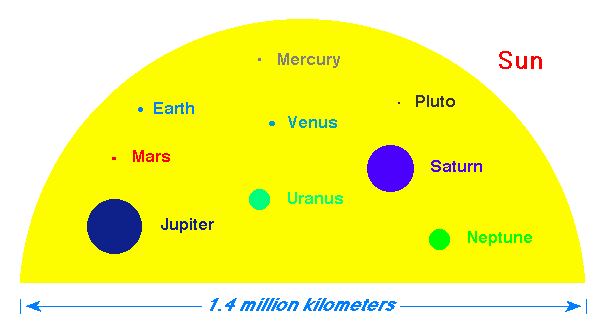
Ambiguity: Yes, Pluto is in the above figure, but it is considered now a "dwarf planet"
The distinction between a "Planet", "dwarf Planet" and "Moon" is made by the International
Astronomical Union (IAU)
Pluto and other large objects in the Kuiper belt do not satisfy the last
requirement as can be seen in the illustration below

The demotion of Pluto from a Planet to a non-planet is not a scientific issue whatsoever - its only a cultural issue.
Rather than dealing with classification names (e.g. moon or planet) its better to stick to physical definitions. Therefore, we will define solar system bodies in terms of their composition and geological properties. In these terms objects come in three categories:
Density is an important physical concept, therefore we will spend some extra time on this subject.
To begin with, the density of planet refers to its bulk density. So even though the structure
of a planet, like Neptune below, might contain many different components of different density,
they all integrate together to produce the bulk density.

The bulk density of any object is its mass divided by the volume that it occupies.
For a sphere, the volume is 

But we only care about the r3 part. If you double the radius of a sphere, you increase its volume by 23 = 8.
So for any spherical object in the solar system its density goes as

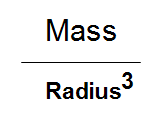
The scaling is important here as we will compute all densities with respect to the density of the earth such that 1 Earth Mass divided by 1 Earth Volume = 1 Earth Density. Or ME/VE = DE, where E refers to Earth units. Alternatively, if given the radius of the planet in units of Earth radii, RE, ME/(RE)3 = DE We want to know how many more times or less times the density of an object is, compared to the Earth. This concept will definitely be tested on the midterm and the final - its fundamental to understanding the physical properties of objects.
So, for example:
If you want to compute the density in proper units then you would just multiply by the density of the
Earth which is 5.5 grams per cubic centimeter (g/cc).
Note that the density of water is 1.0 g/cc.
Let's look at how the properties of the planets and the two largest dwarf planets
in the solar system correlate with distance from the Sun:
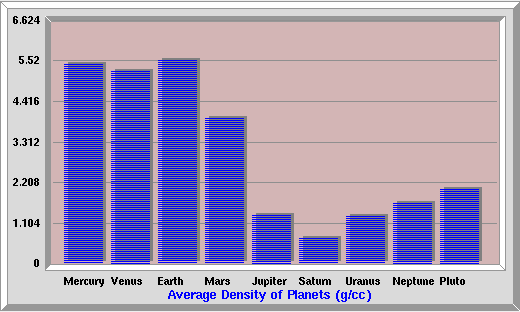
By our density definition we have 2 main groups of objects:
 The reason that density is so important is that it provides an excellent diagnostic of whether or not
an object is primarily made out of rocks, ices or gases.
The reason that density is so important is that it provides an excellent diagnostic of whether or not
an object is primarily made out of rocks, ices or gases.
What can we notice here?
Planet Mass Radius Density Rotation #Moons
(earth=1) (earth=1) g/cc days
Mercury .05 .39 5.42 58d 0
Venus .81 .95 5.25 243d 0
Earth 1 1 5.54 1d 1
Mars .11 .53 3.94 1.02d 2
Jupiter 318 11 1.31 9.8h 15+
Saturn 95 9.5 0.70 10.2h 19+
Uranus 14.5 4.0 1.29 17.9h 9+
Neptune 17 3.9 1.64 19.1h 6+
Dwarf
Planets
Pluto .002 .18 2.03 6.4d 1
Eris .0028 .183 2.52 ?? 1
 Mars: These planets are
called the terrestrial planets (meaning rocklike). They are also
known as the inner planets.
Mars: These planets are
called the terrestrial planets (meaning rocklike). They are also
known as the inner planets.  Neptune:
These planets are called the Jovian planets (meaning gaslike). They are also known as the
outer planets.
Neptune:
These planets are called the Jovian planets (meaning gaslike). They are also known as the
outer planets.
In addition to density, there are other important distinctions between the inner and the outer planets. These include:
These imply outer planets are big balls of gas, compressed by their own weight.
 they haven't been slowed down by tidal effects
they haven't been slowed down by tidal effects
Note: Pluto and other Kuiper belt objects have larger densities than the large gas giants. Effectively they are large rock-ice objects - comets. The orbit of Pluto is also much more eccentric and inclined to the orbital plane than any of the other planets.
All of these distinctions are clues to how the overall solar system formed.