 Physics Emerges
Physics Emerges
 Physics Emerges
Physics Emerges
Recall that Kepler's second law demands that planets move faster in their elliptical orbits when they are closer to the sun. This means that, somehow, the sun can "influence" the behavior of the planet even though there is no direct physical connection between the sun and the planet.
Philosophically this seems strange and this phenomena is generally called action at a distance and is certainly counter-intuitive to our every day experience.
Newton and the Apocryphal Apple:
 "I began to think of gravity extending to the Orb of the Moon,
and having found out how to estimate the force with which a globe revolving within a sphere
presses the surface of the sphere. From Kepler's Rule of the periodical times of the Planets,
I deduced that the forces which keep the Planets in their Orbs must be reciprocally as the
squares of their distances from the centres about which they revolve : and thereby compared the force requisite to keep the Moon in her Orb with the
force of gravity at the surface of the Earth, and found them to answer pretty nearly".
"I began to think of gravity extending to the Orb of the Moon,
and having found out how to estimate the force with which a globe revolving within a sphere
presses the surface of the sphere. From Kepler's Rule of the periodical times of the Planets,
I deduced that the forces which keep the Planets in their Orbs must be reciprocally as the
squares of their distances from the centres about which they revolve : and thereby compared the force requisite to keep the Moon in her Orb with the
force of gravity at the surface of the Earth, and found them to answer pretty nearly".
Newton postulated that there was an attractive force between the Sun and the
planets that had to account for Kepler's third law. Knowing that the Kepler's second and
third laws meant that the orbital velocity of a planet must be a function of distance from the Sun,
Newton deduced the functional form of the gravitational force law that would be required to
reproduce these laws. As Newton was able to show, Kepler's third law requires that the gravitational
force between two objects decrease as the inverse square of their distances.
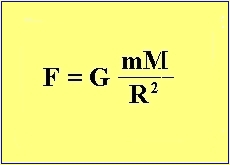
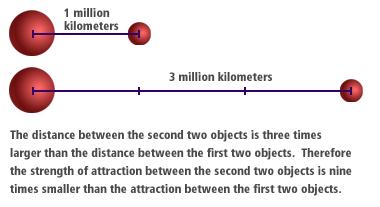
Note the key dependence on the inverse square of the distance.
|
Step 1:
Assume that M1 is a small mass in a circular
orbit about a much larger mass M2 . We can write down the Force
law on M1 using Newton's formulations:


Step 2:
Combining terms yields:
Step 3:
In an orbit governed by a central force, the
centripetal acceleration, a is given by:
Step 4: For a circular orbit, the circular velocity, Vc is the total distance traveled (the circumference of the circle) divided by the orbital period, P or Vc = 2p R/P which then yields:  |
Measurements of R and P for any lesser body
( M1 ) in orbit about a larger body ( M2 ) now gives directly
a physical quantity, mass.
a body remains at rest or moves in a straight line of
constant velocity as long as no external forces acts on it  this helps us get to the moon
this helps us get to the moon  this is why good
fuel economy basically requires a reduction in mass of the vehicle
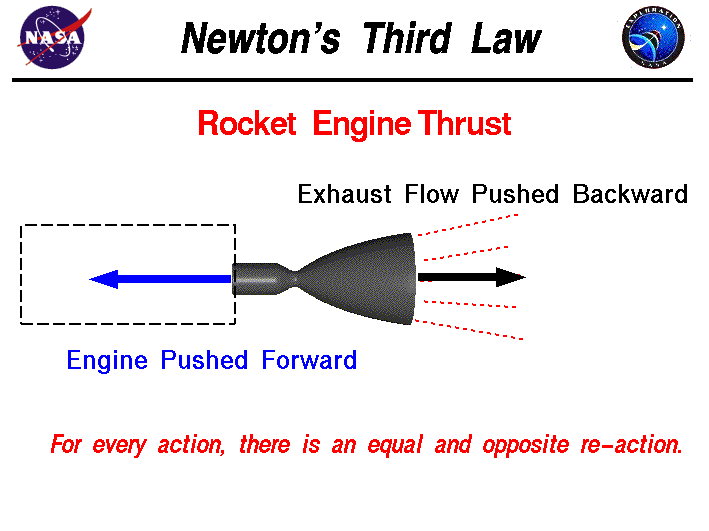
this is why good
fuel economy basically requires a reduction in mass of the vehicle  for every action there is an equal and opposite
reaction
for every action there is an equal and opposite
reaction  Newton's third law is often hidden in the macroscopic
world due to friction. If you want to experience Newton's third law, put your
self in a frictionless environment.
Newton's third law is often hidden in the macroscopic
world due to friction. If you want to experience Newton's third law, put your
self in a frictionless environment.
Newton also realized that a combination of all these three laws implied an important
physical tenet  The Conservation of Momentum.
The Conservation of Momentum.
The momentum of an object is simply expressed as: mass * velocity or just mv
Conservation of momentum states that whatever the total momentum of the system was before any event or interaction occurs, the total momentum of that system after the event or interaction occurs will be unchanged. Indeed, this principle actually gives rise to the necessity of newton's third law.
The genius of Newton was his ability to
use calculus and coordinate transformations to reveal the underlying
physics.
Calculus as a Language
For example, how does one compute the area of a circle?
A circle is a figure enclosed by a surface which a line of
radius r has been rotated through 360 (2π) degrees.
From the language of Calculus this means the following:
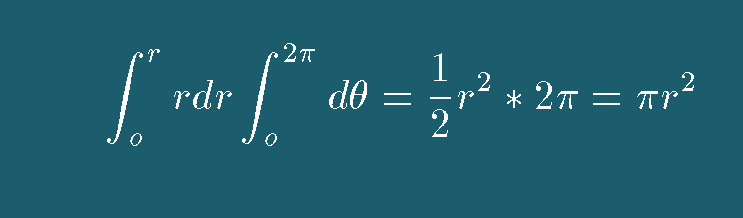
Language should evolve so that communication becomes more efficient; i.e. the above graphic shows how to derive the area of a circle in the least amount of steps
His place in the Gravity Hall of Fame is not due to his discovery of gravity, but rather due to his discovery that gravitation is universal. ALL objects attract each other with a force of gravitational attraction.
Upon this realization, Newton's first thought was this:
Well fine, if gravity is an attractive force, then how come the
Universe is still here?
Okay then, how come the
moon doesn't come crashing into the earth, or the earth into
the sun.
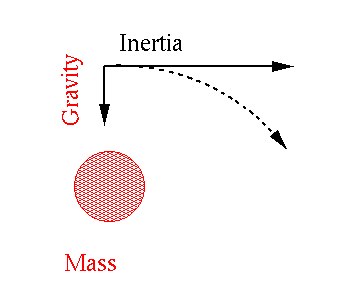
What causes an orbit to be stable?
An orbit is the balance between inertial (Newton's First Law) and gravitational forces (Newton's second law). That is,
the earth is continually falling toward the sun, but inertia also wants the
earth to keep moving in a straight line. When these two forces are in
balance a stable orbit results:
Newton's Universal Gravity
Important Physics Note
It took Newton a fairly long time (10 years or so) to recognize that gravity behaves as if the mass of an object (e.g. the Earth) were all concentrated in its center. For a long time, Newton thought that Gravity emanates from the surface of the Earth. However, since the center of the moon is farther away from the center of the Earth than the respective surfaces (by 2.5%), Newton could not get the orbit of the moon to agree with observations unless the force was computed based on the distances between the centers of the two objects rather than the surfaces.
Later on, Newton reliazed that this idea of "point masses" was easily proveable using his Calculus.