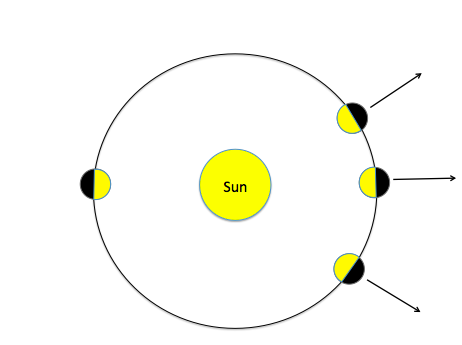
The Celestial Sky: A Coordinate System

Motion has no meaning with out a coordinate system. Indeed, physics can't be described without a coordinate system and measurements don't mean anything without a coordinate system. Events don't occur without a coordinate system because an event is something that occurs at a specific time in a specific place.

For instance, if you text message your friend the following:

Meet me then nothing happens. If you specify a coordinate:

meet me @ *$

still nothing happens because you have not specified a time, only a location. Hence our coordinate system for events consists of a location plus a time; otherwise known as spacetime.

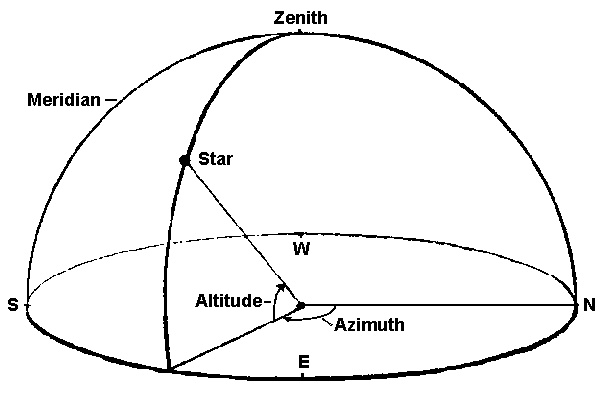
Altitude-Azimuth Coordinates

For an observer standing on the surface of the earth, the simplest possible coordinate system for observing the motion of a star is shown below:

In this diagram, an observer is standing in the middle of the hemisphere shown above. The disk the ground and the perimeter defines the horizon. The dome is their view of the sky. This model assumes that the earth is flat (with respect to the observer) and since the radius of the earth is a lot bigger than your height of 1.8 meters, this assumption is valid.
Directly overhead the observer is zenith. Imagine a line from the center of the Earth that continues through the observers's body through the top of the observer's head. This line points to zenith.
A star will rise in the east and set in the west and at any given time it will have some height about the horizon (e.g. ground) which corresponds to the angle between the star and the horizon. When the star is directly overhead at zenith, that angle is 90 degrees. This angle is called altitude.
Azimuth is the coordinate direction that runs parallel to the horizon and rotates clockwise from north (0 degrees) to east (90 degrees) to south (180 degrees) to west (270 degrees) back to north (360 degrees). Yes, north can be defined as 0 or 360 degrees. For example, a star located precisely in the south east would have an azimuth of 135 degrees.
The star in the diagram has an (estimated) altitude of 45 degrees and azimuth of about 120 degrees.
The meridian is an imaginary North-South line running through the zenith. As the star approachs the meridian it is still "rising"; at the meridian its at its highest altitude in the sky; as the star continues its motion it approaches the western horizon and moves away from the meridian and is thus setting.
It should be apparent that this system is based on the observers location on Earth. Screenshots below from Stellarium show Alt-Az coordinates of Rigel taken at the exact same moment in Calgary and Los Angeles. The viewing direction is the same in the sky yet the Alt-Az coordinates and position of Rigel are different. For early astronomers like Tycho Brahe, this was a useful coordinate system to measure the position of Mars night after night from one location on Earth. However, for modern astronomers it is infinitely more convenient to define a coordinate system independent of an observers location on Earth. Thus Rigel can have one coordinate associated with it rather than a multitude that depend on location and time on Earth.

Celestial Coordinate System - RA and Declination

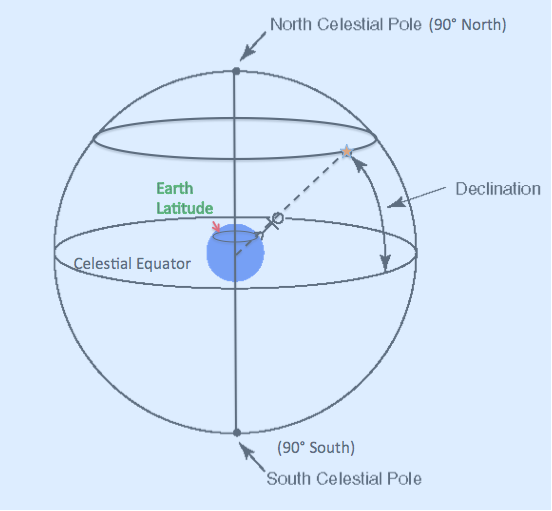
This improved coordinate system defines a celestial equator as a projection of Earth's equator in the sky. North and South celestial poles are +/- 90 degrees from the celestial equator. These are also projections of Earth's North and South poles into the sky.

Celestial coordinates are defined as a system where the celestial equator is a projection of the Earth's equator. The Celestial poles are projections of Earth's north and south pole. Thus any star reaching its maximum altitude at zenith for an Earth observer would have the same declination as the observers latitude on Earth.

In this coordinate system, an observer at some latitude would observe that any star reaches a maximum altitude in the sky. That maximum altitude is equivalent to the latitude of the observer and is known as declination . Thus if you were on a sailing ship and had a list of declinations of brightstars and measured when those stars reached their maximum altitude, you would then know your latitude. One particular star convenient for measuring Earth position is the North Star or Polaris. It remains fixed hour after hour, night after night. For example if you were on Earth and saw Polaris at zenith, you would be located at the North pole. If you saw Polaris at 30 degrees above the horizon, your latitude would be 30 degrees north. Now for any star reaches its maximum altitude at point lower than the observers zenith, the latitude is equal to 90 - star altitude + star declination. For example Suppose you view a star reaching maximum altitude 65 degrees above the horizon, you know that its declination is 20 degrees north, thus your latitude is: 90 - 65 + 20 = 45 degrees north.

Knowing your longtitude, however, would require a universal time system on the Earth and that is not established and defined until the 19th century (1884 to be exact). The sky equivalent to longitude is Right Ascension or RA. This coordinate is divided into 24 hours (no coincidence there) or 360 degrees. There are 15 degrees to one hour. 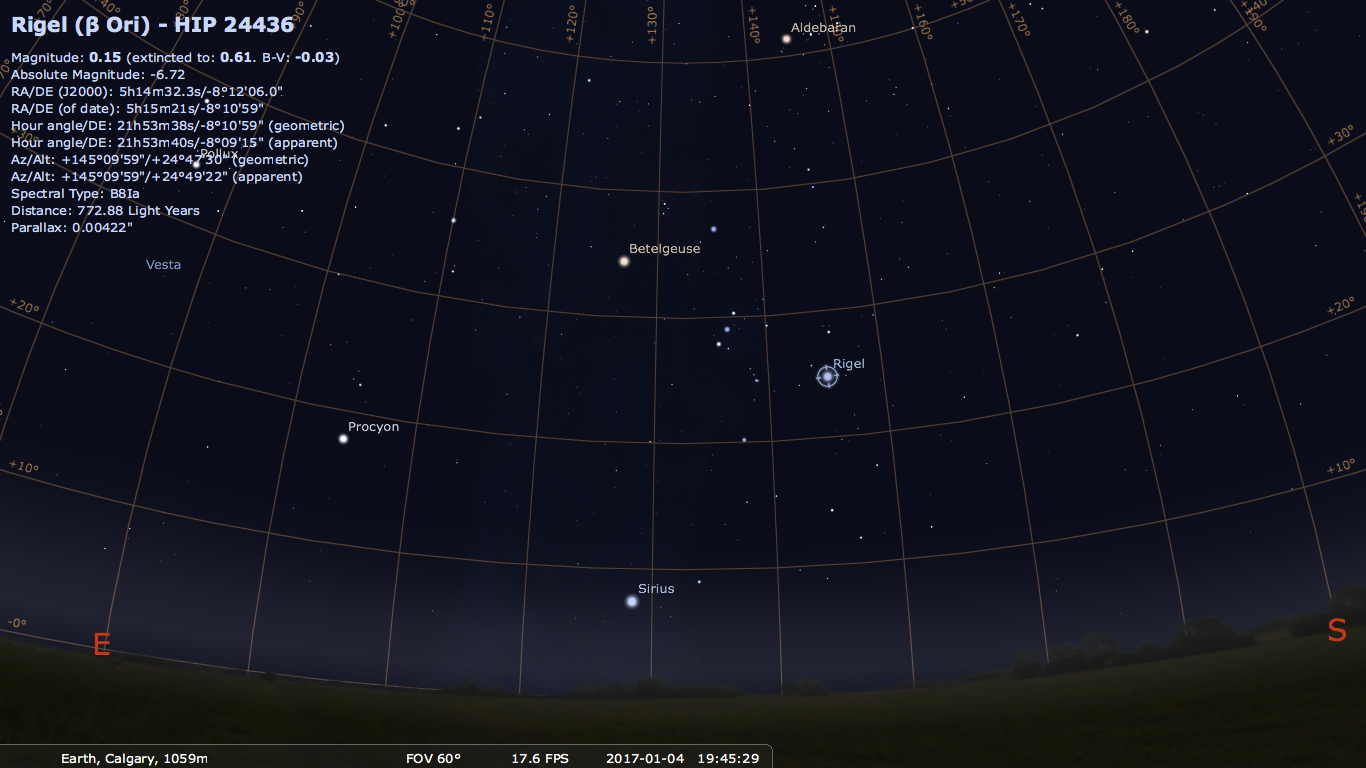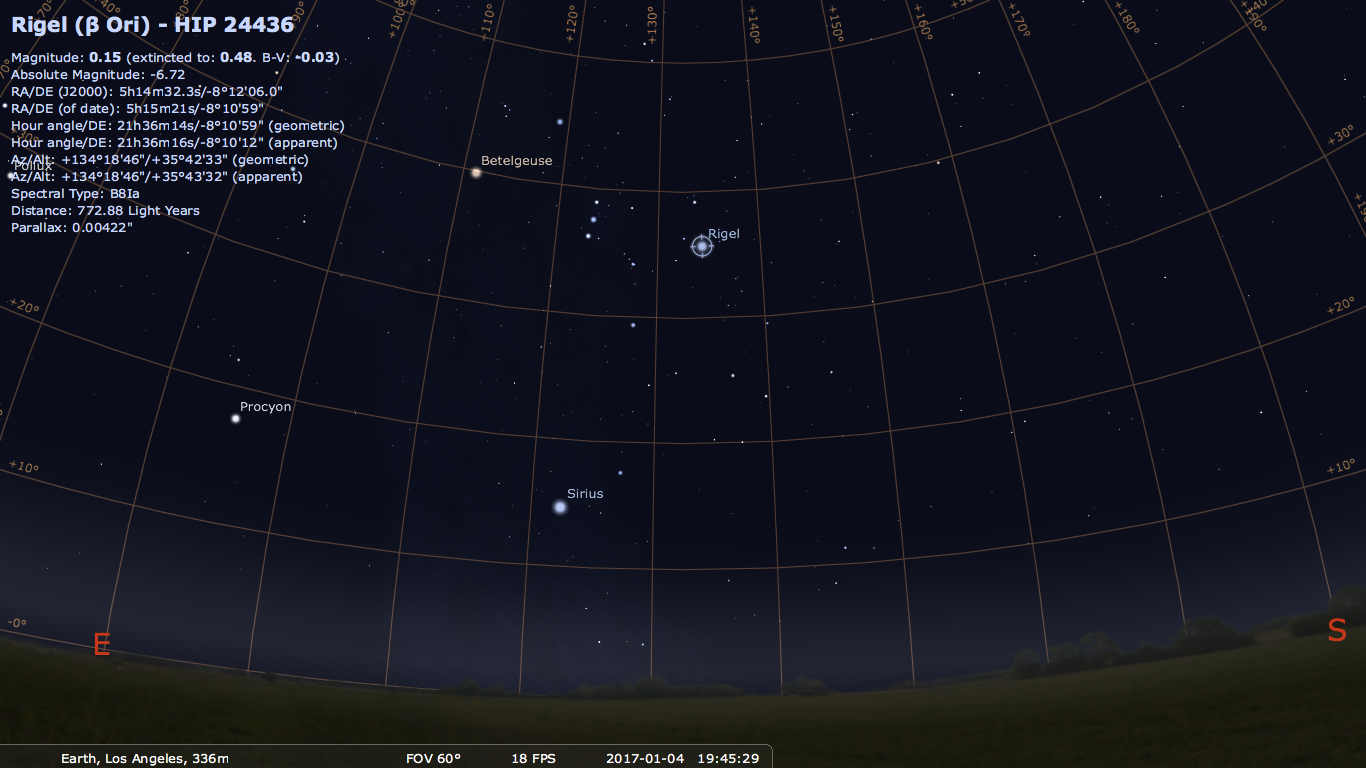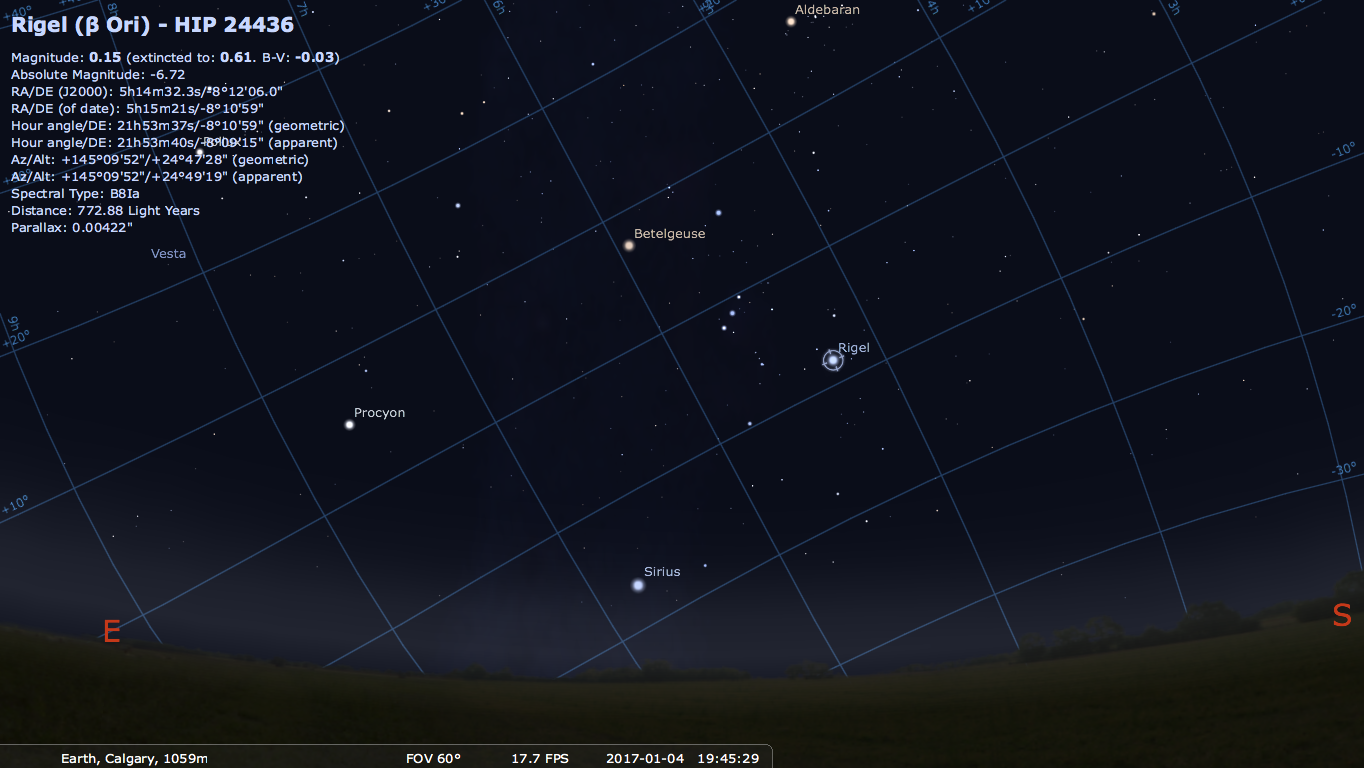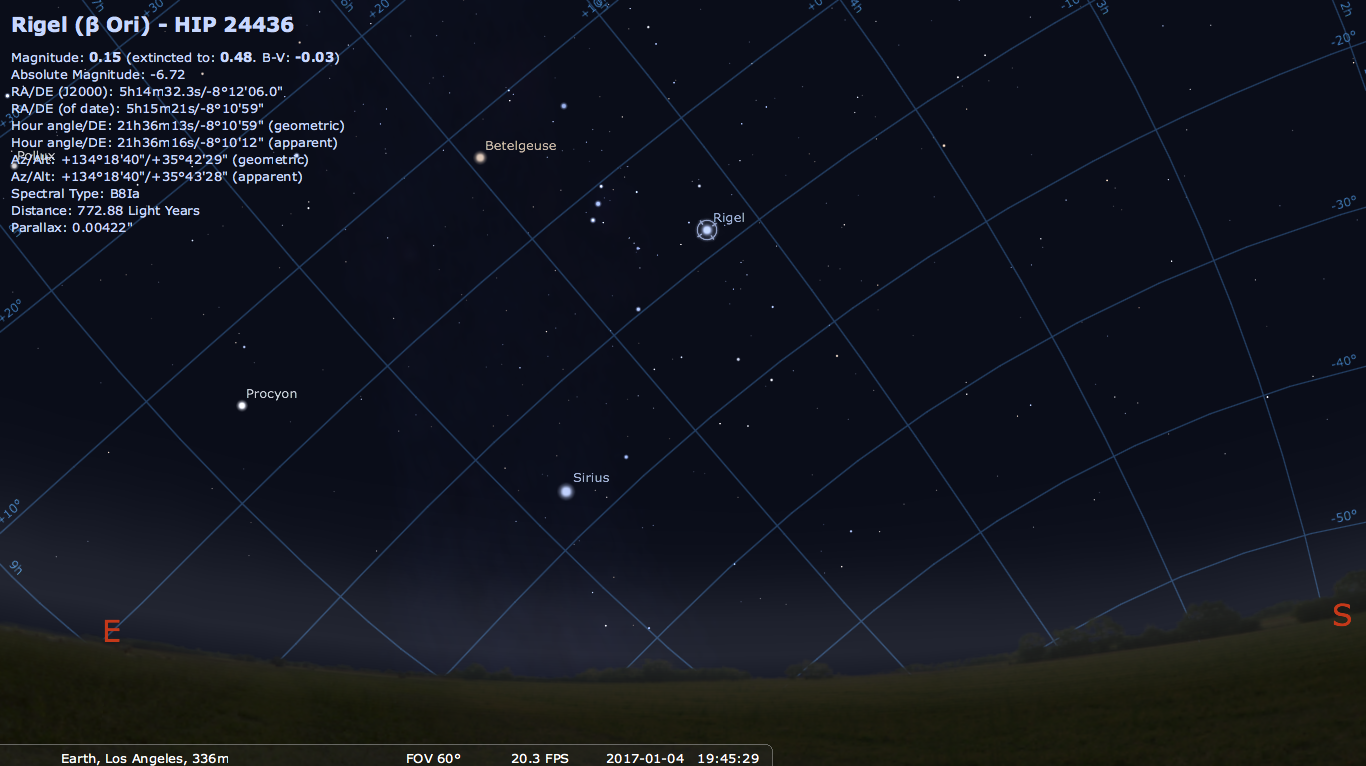Thus if you stare at one fixed direction in the sky, the stars will have "moved" 15 degrees in one hour in RA. Below shows Rigel in the RA Dec coordinate system for Los Angeles and Calgary. Notice that the RA/Dec coordinates are the same for both locations. Yay!

As mentioned, this coordinate system is the most commonly used sky coordinate system for astronomers. Stars remain fixed to this coordinate grid with small adjustments every 50 years due to Earth's wobble. Yet the Sun moon and planets do not have fixed RA and Dec coordinates like the stars. And it still can not explain why the amount of time the Sun spends in the sky varies.

A simple experiment done initally by chinese astronomers around 1000 BC gives a clue as to why the sun varies and all you need to do is put a stick in the ground:

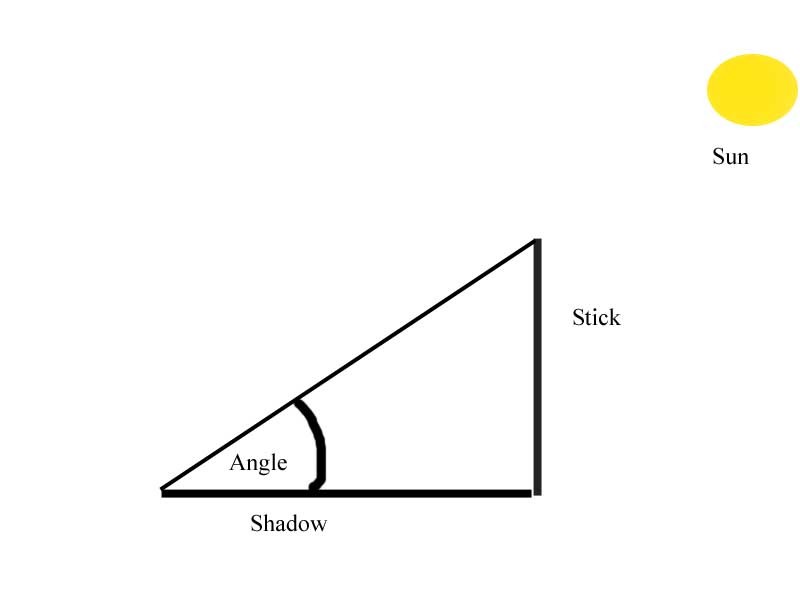
If you do this, you will notice that at solar noon (when the sun is at its highest point in the sky) there is a shadow of a certain length from which you can measure an angle. If you do this long enough (e.g. for one year) you will notice there was a maximum angle measured and a minimum angle measured (this works for any latitude).

The difference between those maximum and minimum angles will be 47 degrees. This difference is equal to twice the "tilt" of the Earth. Therefore the earth has a "tilt" of 23.5 degrees.

But a tilt with respect to what?

The correct understanding of tilt requires a different coordinate system

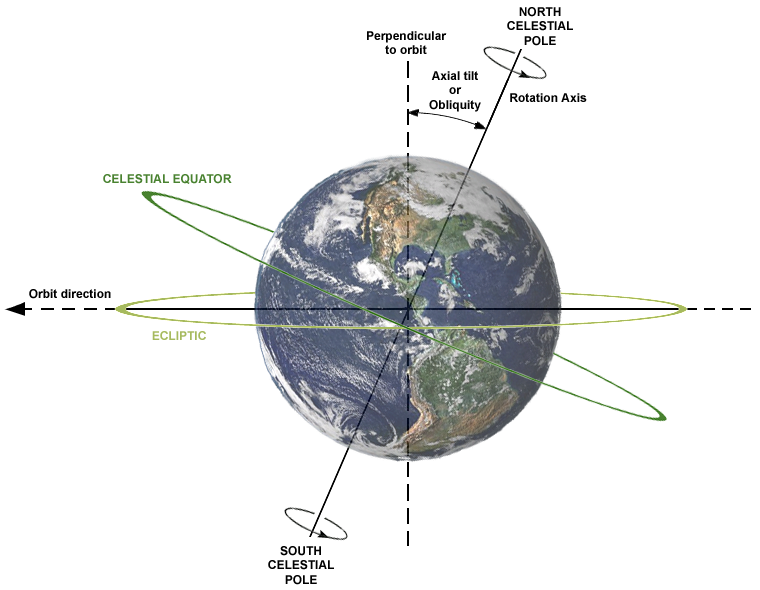
Which establishes the "horizon" as being an extension of the equator of the sun. This is known as the ecliptic plane and we will see later that all of the planets orbit within this plane. Thus the tilt of the earth means that its rotational axis is titled by 23.5 degrees with respect to the equator of the sun (or equivalently, the ecliptic plane).

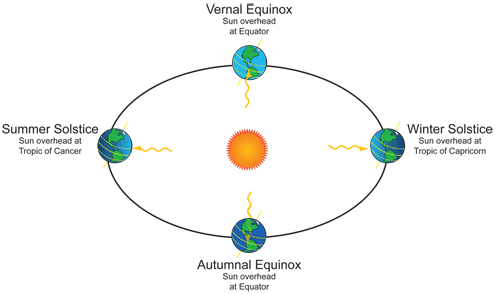Earth's tilt with respect to the Sun at different times of the year (Image credit: NASA/NOAA).

So from the point of view of an observer on the ecliptic plane, the equator of the Earth is tilted by 23.5 degrees.

Since coordinate systems are often relative then they can be shifted. So from the point of view of the observer on the Earth, the ecliptic plane is tilted by 23.5 degrees relative to the Earth's equator:

So this means that in the summer solstice the Sun has a declination of 23.5 degrees, meaning that if you were at 23.5 degrees the sun would be directly overhead (e.g 90 degrees above the horizon) at noon.

Now finally, let's consider the case of Eugene, which is at a latitude of about 44.5 degrees.

44.5 - 23.5 = 21 degrees away from that reference point
On the summer solistice the maximum elevation of the Sun above the horizon would therefore be 90-21 = 69 degrees.
At winter solistice, the sun has a declination of -23.5 meaning that if you were at -23.5 degrees south latitude, the sun would be 90 degrees above the horizon. Eugene would be 44.5 - (-23.5) or 68 degrees away from that reference point -so on Dec 21 in Eugene the sun have a maximum angle above the horizon of 90-68 = 22 degrees.
At the time of the equinoxes the sun has a declination of O degrees meaing its directly overhead at the equator or, in the Eugene sky, has a maximum altitude of 44.5 degrees above the horizon.

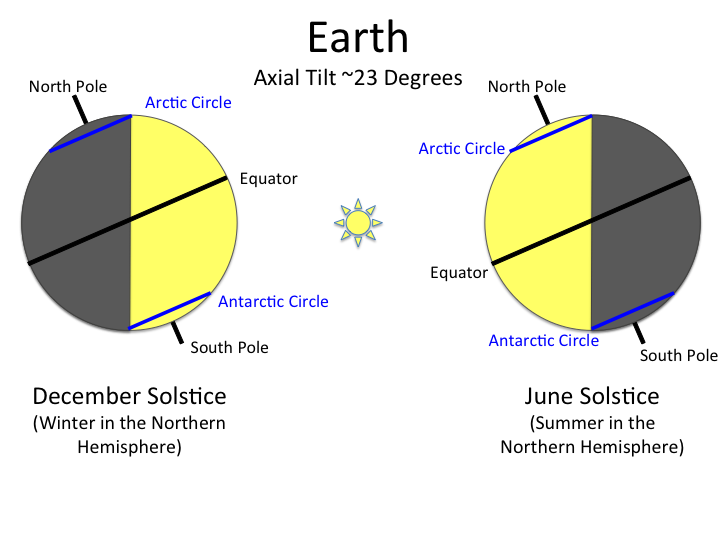Detail of Earth's Tilt at Winter and Summer Solstice (Image credit: NASA blogs).

Changing Night Sky

As the Earth orbits the sun it moves approximately 1 degree every day. As it moves, midnight which by definition is 180 degrees from the sun, changes direction with respect to an observer in the ecliptic plane.

As a result, you get different constellations at midnight depending on the time of year.