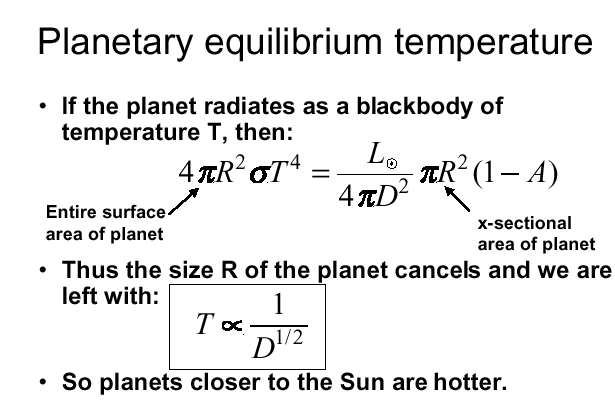
The simplest case is a planet without an atomsphere so we start with that and simply balance received flux vs outgoing flux. The received flux is simply:




For the earth, the atmospheric albedo, which is entirely produced by reflections from cloud tops, is approximately 0.3.

What we wish to do is to derive a simple expression for how the atmosphere modifies the temperature of a planetary surface

Before doing this, we need to make some assumptions about our atmosphere.

• The atmosphere is Thin

• The atmosphere is supported by pressure equilibrium (hydrostatic equilibrium)

• The atmosphere is isothermal

• The equation of state is the Ideal Gas Law

These assumptions allow us to treat the atmosphere as a thin, uniform slab of material at constant density and temperature.

First some constants:

• Solar Constant:
  
  
  • F_o = Flux at the top of the Earth's atmosphere = 1370 watts per square meter (W/m²)

  • Stefan-Boltzmann constant s = 5.67 x 10^-8
    
    
    
    

Going back to the planetary equilibruim temperature we see that

4σT⁴ =F_o(1-A)

or

T⁴ = ((1/4*1370)/σ)(1-A)

T = 278*(1-A)^1/4

For A = 0.3 one gets T = 254K