How fast will Resource X be depleted? - Seems like a simple question and a question that might be important answer in a reliable way. Yet, in general, we do bad at this as well. For example, suppose we have the following situation:

• As of 2013, there are 100 units of Resource X still available to us
• In the year 2013, we will use 1 unit of Resource X.
• as measured over the last 6 years, our use of Resource X grows at the rate of 5% per year.
  
  

Dear Congressperson, when will resource X run out.

Congressperson says "oh don't worry, Resource X will be around for 100 years because 100/1 (R/r) = 100 - even I can do that math - and I will just ignore that small 5% deal that you claim exists"

Well, does ignoring that matter or not?

Clearly, Exponential growth, in general, is not understood by the lay public. If exponential use of a resource is not accounted for in planning - disaster can happen. The difference between linear growth and exponential growth is astonishing. Exponential growth means that some quantity grows by a fixed percentage rate from one year to the next.

In this animation, one can clearly see that no matter what the growth rate is, exponential growth stars out being in a period of slow ( and looks LINEAR during this period growth and then quickly changes over to rapid growth with a characteristic doubling time of 70/n (n = annual % growth rate; e.g. 70/5% = 14 years).

Hmm, I wonder if there is a way to find out if ignoring the growth rate in resource use actually matters. Why yes there is!:

The correct equation for calculating the exponential exhaustion timescale (T_e) of any resource (should be required knowledge for any one elected to congress):

T_e = 1/k * ln (Rk/r_o +1)     The derivation of this equation

where k = growth rate
R = total resource available
r_o = initial consumption rate

Back to congressperson speak:

"Gee that's a complicated equation I am not sure I understand it nor how to use it (don't worry there's in app for that) so I think I will just continue to ignore that. Life is much simpler when everything is linear and honestly, I don't think the 5% growth rate is a big deal. So I use 1.05 units next year, I still have about 99 left - what's the big deal"

Well, let's first consider that question in a historical context. 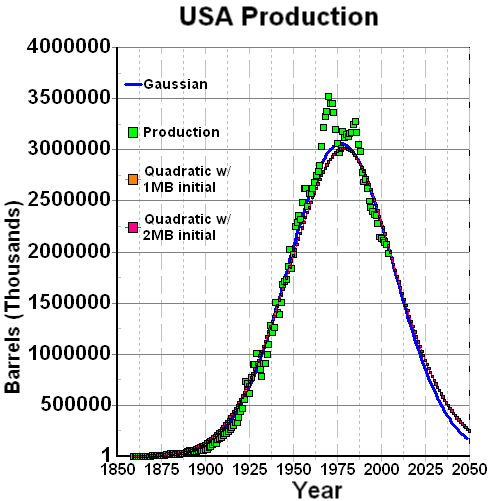Let's start out with the curve for US Oil production in the lower 48 States. Note that peak production occurs on a timescale of 1/2 of T_e as the production curve is assumed to be symmetric. In the real world, when resources reach peak production, prices tend to go up which can then serve to lower consumption and extend the exhaustion timescale.

In 1956, M. King Hubbert published an ignored paper based on this methodology as applied to US Oil production. In that paper he assumed the following:

• Measured Growth rate of oil production in the US over period of 1945-1955 was 3% (.03)

• Starting period of calculation is 1946

• Hubbert estimates the ratio of R/r_o in 1946 to be 120

He then published his 1956 paper which predicted that the lower 48 states would reach peak production in 1971. Of course, no one believed him at all and he was not taken seriously even though his methodology was secure and he even turned about to be correct (which usually happens when you characterize the problem correctly from the outset)

We can gain further insight on this methodology by using the following "app" Excel template

When you first open the spreadsheet you will see the 5% growth rate scenario that starts with R/r = 100. Please now mail your congressperson to tell them that you run out of resource X in 36 years not 100 years. Gee, I guess that 5% thingie does make a difference ....

In the following examples you are to only change the value that are in cells A2, B2, and C2. If you change any of the others that you have overwritten the formula for that cell and will have to re-download the spreadsheet to continue,

Examples to do in this template:

1. Do Hubberts original one with start year = 1946, k =.03 and R = 120. et voila 1971 appears as the Peak Year
   
   
2. Now you have just posted this result on your blog and you ignite a flame war as Mr. BigOil says that you are full of shit and there is twice as much available oil as you think there here is. So, put 240 into the spreadsheet and what do you get for the peak year? A mere 10 years more (1981). Why is this? Well, its because the peak year depends on the natural logarithm of R/r and not on R/r directly and ln(R/r) is smaller than R/r. This is simply not understood by congresspersons or BigOilMen or most students and its the reason that all of this is not intuitive (but it is correct).
   
   
3. Now let's consider the case for "peak oil" or the exhaustion time scale for oil. Remember that in the real world we are at plateau oil because we are refinery limited. The calculations you will do below assumes that are not limited by this.
   
   
   • Make the start year 2010 and R/r = 50 and let k=0.03. When do we run of oil under that scenario?
     
   • Now make k=0.05 to account of emerging markets. When do we run out of oil now?
     
   • Now let's mine the crap out of the deep sea sediments in the Gulf of Mexico to support that 5% growth rate (and have a few Deep Horizon incidents as the cost of doing business) so that we can triple R/r (to 150). When do we run out now? Is it really worth the effort to do that?
   
   
   What about the case for Natural Gas which is a booming new fuel source as of 2010, how long will the boom last? NG use is growing worldwide at a rate of about 6%. R/r is 70 for this resource. How long does the boom last?
   
   The Exhaustion of Steel:
   
   The most serious material scarcity that the world faces (but again no one believes) is that of steel. Steel is still the main building material for almost all the world's infrastructure. Eventually steel will be replaced by carbon fiber but that is at least 50 years away.
   
   Steel is basically Iron Ore plus some alloy (zinc, tin, manganese) and among these, manganese is the most widely used alloy.
   
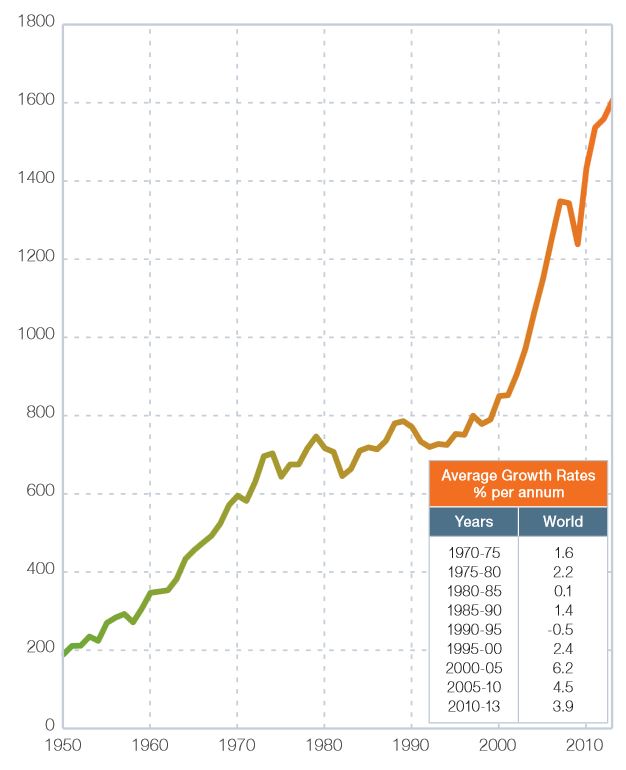
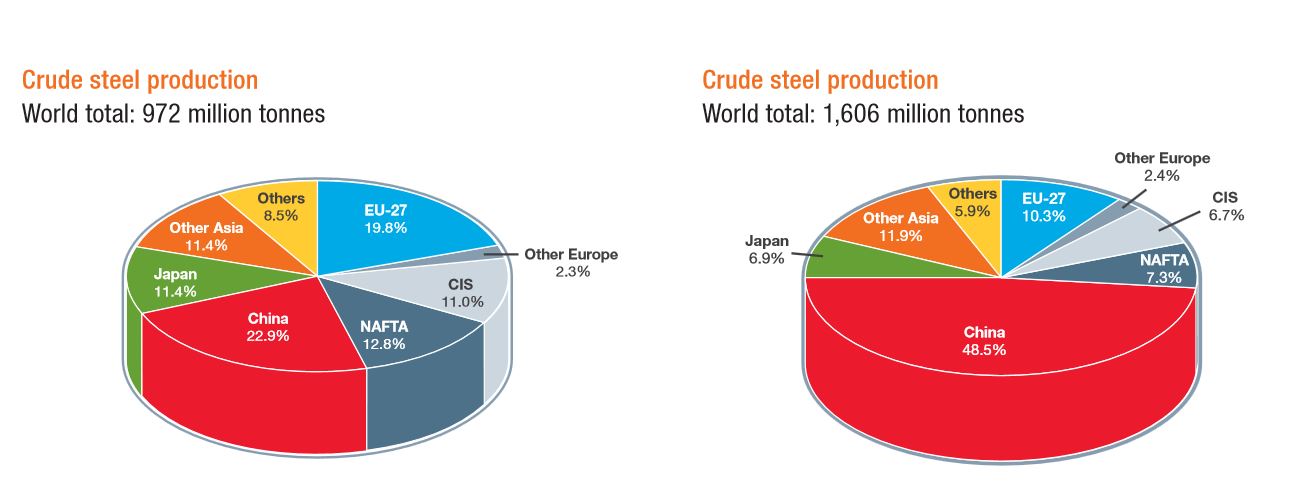
   Averging together a few estimates suggests that in the Year 2012, R/r for steel was 150. The global rate of usage of iron ore for the making of steel is shown below along with an inset that shows the growth rate in various 5 year periods. Clearly the growth rate in each period is different (due to market and demand conditions). However, while it once appeared that the use of steel was leveling off (1980--2000) from an earlier steep rise, the emergence of China has strongly changed the steel market and if it weren't for the global economic meltdown of 2009, the rates would be even higher. Currently the world demand for Iron Ore exceeds the available supply. This has lead the development of new projects like The Mesabi Nugget Project
   
   
   
   
   
   So for steel exhaustion we can envision three scenarios starting in 2013 with R/r = 150:
   
   
   • Maintain current growth rate of 3.9%
   • Use 10 year averag of 4.7%
   • Assume market driven growth rate of 6.2% (e.g. 2000-2005 figure below)
     
     
   
   
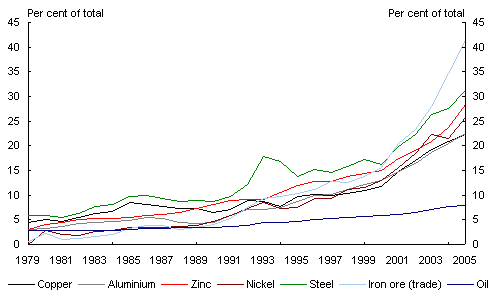
   The issue of steel production is directly associated with the reserves of Manganese that are available. This information can be found here: Manganese For the case of manganese use in the production of steel, R/r is about 40 so go back into the spread sheet and use 40. Are we screwed or what?
   
   Clearly manganese based steel is on the verge of running out which has created a strong increase in the price of manganese in world markets. This is the general market reaction when you get past peak production. The chart below shows the global manganese market over the last 8 years. You can clearly see the factor of 3 price increase from 2005 to 2007! That then was impacted by the global economic meltdown (history will show just what a big deal this actually is) as construction slowed down and demand for manganese went down and so did the price.
   
   
   
   
   
   Maganese Reserves are dwindling while production of steel is increasing. This is what drives resource scarcity as determined by Hubbert's methodology.
   
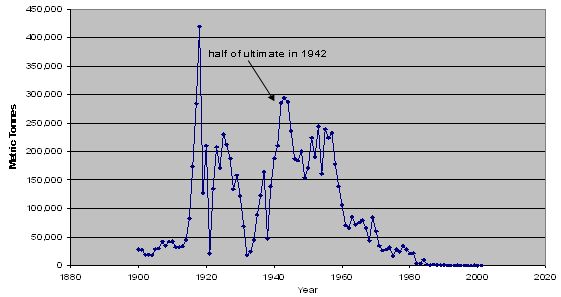
   As the graphic below shows, the US no longer produces Manganese (Mn)and so we have to import this in order to make Steel in the US:
   
   
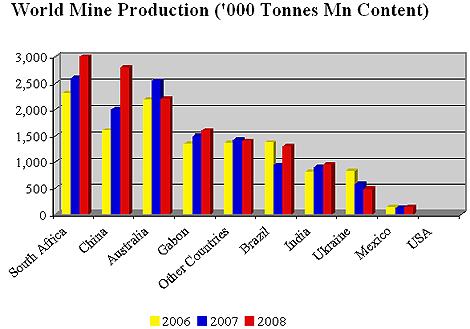
   In fact US MN production stops in 1980!
   
   
   
   

   
   
   
   So on the surface, application of Hubbert's methodology strongly suggests that the world is going to experience peak production on a variety of mineral and other resources. Various economic corrections will then occur and prices will dramatically rise as a result of real, global, scarcity.

   Back to Congress:

   The basic problem is that we substitute Disney's First Law for this arithmetic reality of resource depletion.