Rossby waves are planetary waves that determine basic meteorological conditions at latitudes outside of the tropics.

Rossby waves are an essential conseuqence of

• Planetary Vorticity must be conserved
• The coriolis force varies with latitude - this is known as the β effect.

Rossby waves have several important features:

• They redistribute momentum and transmit energy
• They interact in complex ways with the general circulation.
• They delay effects of climate events and their natural system timescales generally produces peristent weather on the scale of 3-5 days.

What is Planetary Vorticity and why must it be conserved?

Vorticity is generated in the atmospheric and ocean fluids by the rotation of the earth since these fluides can't co-rotate with the earth because of internal currents and friction and various energy losses. Vorticity is a measure of spin.

Any air parcel that is stationary relative to the Earth's surface will acquire planetary voriticy as it changes latitude. At the equator voriticy is zero and maximizes at the poles.

We define the planet to have net positive vorticity since it is rotation in one specific direction.

Relative vorticity is produced by two main effects:

• latitude migration (curvature of earth)
• velocity shear

The sum of a parcel's planetary vorticity and its relative vorticity is called the absolute vorticity

East of the any large scale vortex there will be divergence and upward motion of the air. West there will be convergence and downward motion. This often produces clouds and precipitation.

Parcels displaced northward in latitude will achieve negative relative velocity and therefore, to conserve planetary vorticity, parcels have to then move south to increae positive relative velocity. This is why this is a planetary wave and at any given time there me be 3,5 or 7 of these Rossby Nodes:





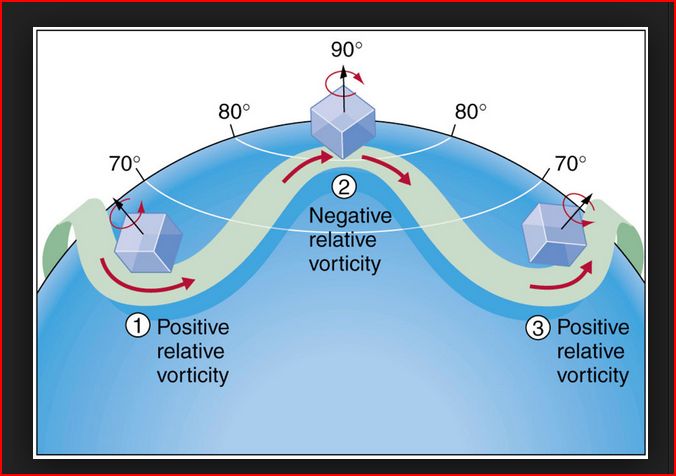
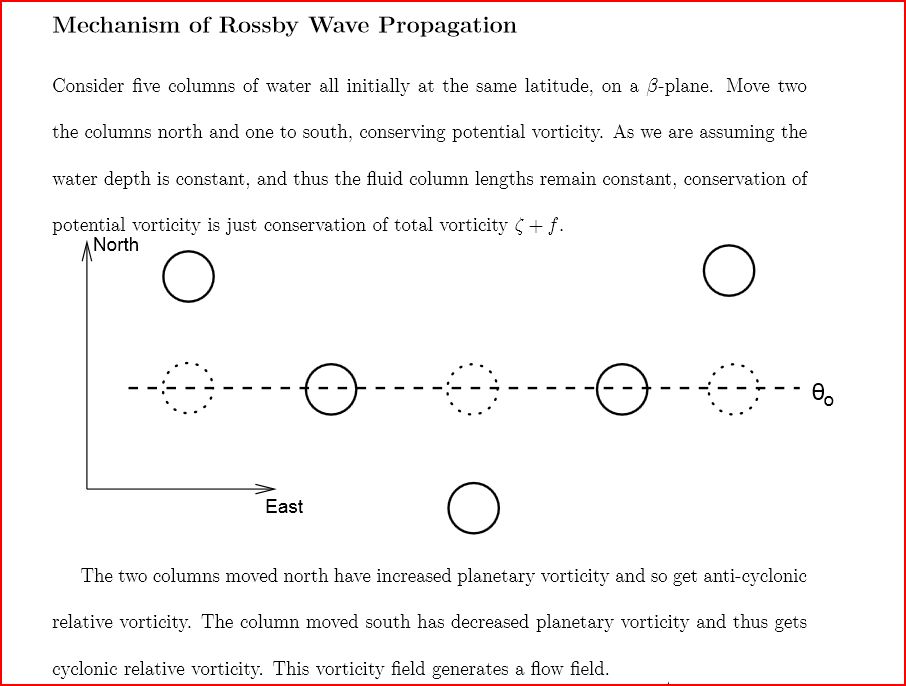
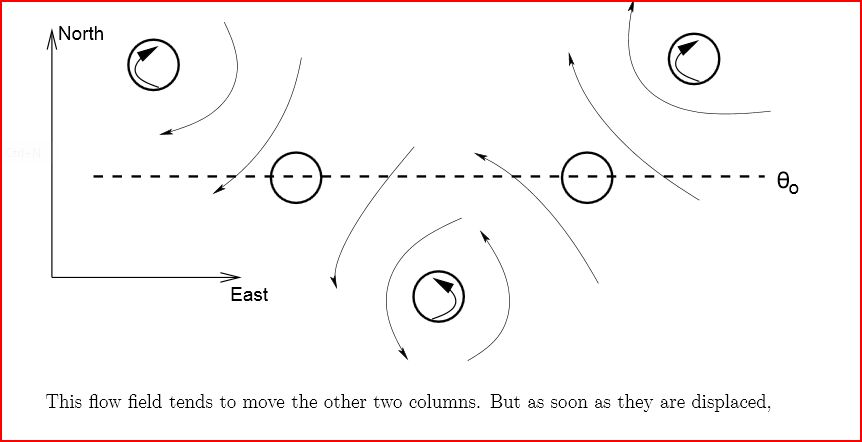
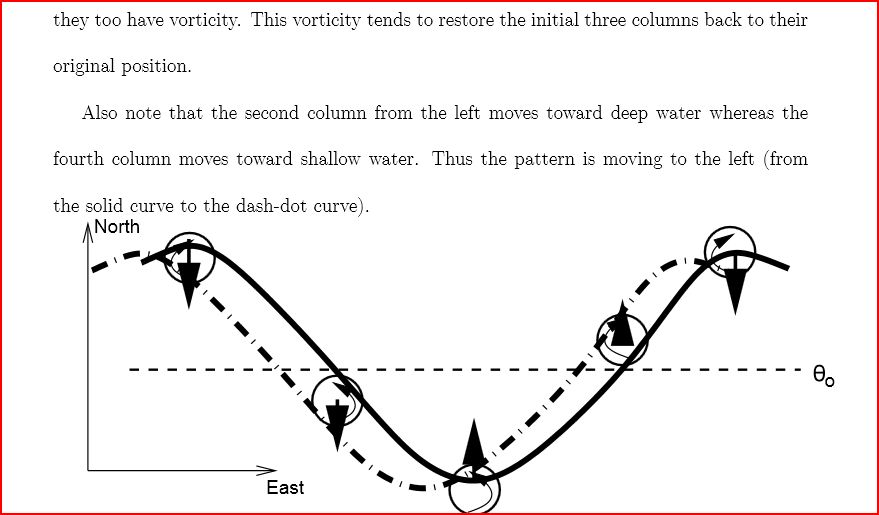
The increase in vorticity is because f (planetary vorticity) has increased compared to the relative vorticity ζ because the "circumference of the earth" is lower at high latitude.





The Coriolis parameter f = 2Ω sin θ can be expanded using a taylor series around θ = θ_o This expansion is useful since a real vortex will span a range of latitude and hence second order effects become important.




Note, this general behavior is the same in water (ocean) as it is in the atmosphere and it again is driven by the conservation rule: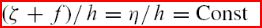

We can write down the momentum equation in one dimension where the RHS is something we have seen before in terms of cyclostrophic balance. Remember η is the absolute vorticity.




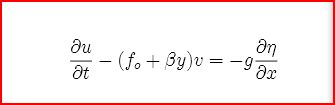
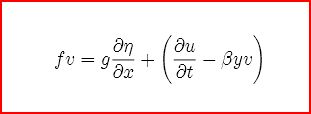
This is basically the geostrophic condition when voriticy is included and that vorticity is mostly generated by latitude migration of weather systems(the β effect).

Very thorough Rossby Wave Primer