Now because μ_s depends on pressure then Γ_s depends on the temperature and pressure. The numerical value for μ_s requires knowing e_s which we can calculate from the Clausius-Clapeyron equation which is coming up next.

However, its far easier to write a simple computer program and generate lines of contant Γ_s in the temperature vs pressure plane and just read off the graph:



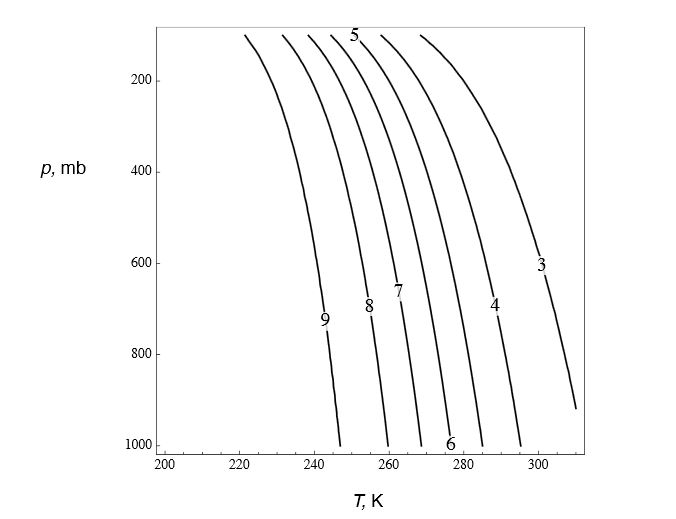
For example, at p = 1000 mb and T =288K, Γ_s ~4.7. Note that as T increase Γ_s decreases as there is more available water vapor, e.g. μ_s is bigger.

Finally here is a simple numerical example:

From before we have



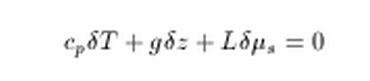
dividing thorugh by c_p shows that ΔT depends on the g/c_p term (~ -10k/km) but also an additive term for latent heat of LΔM/c_p where ΔM would be the physical mass of water vapor than condenses.

L ~ 2.5 x 10 ⁶; c_p ~ 1005

So if you had 1 kg of dry air rising from 0 to 3 km that would experience ΔT = -30K.

If I had 6 grams of water vapor condense (which corresponds to a partial pressure of e =μp/f ; p = 1000mb; e ~10mb); then the corresponding heat release would be:

ΔQ = 2.5 x 10 ⁶ *.006/1005 ~ +15K

so the total change is now only -15K during the rise to 3 km. Hence, water vapor condensation is a MAJOR source of heat input into rising parcels of air.