Problem 1:

Suppose air moves inwards in a tropical cyclone but the air temperature means equal between the cyclone and the environment at T = 302K

Over some time period (5-7 days) the air presssure in the cyclone drops from 1010mb (p₁) to 920 mb (p₂).

How much heat is added to each kg of air?

We had earlier (see dry adiabatic lapse rate) derived a condtion of δQ: ΔQ = TΔS



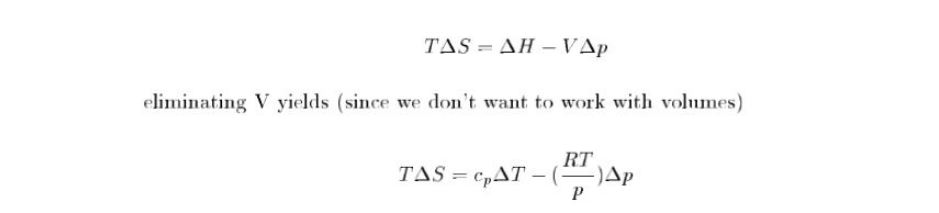
Now since there is no temperature change (ΔT = 0) then we are left with:



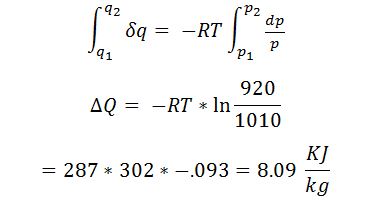
Problem 2:

What is the buoyancy of the air in the interior compared to the environment? (remember to multiply units of millibars by 100, always).



This indicates that the bouyancy force, driven by pressure variations alone, is generally small (compared to gravity). This is why the the upwards motion in cyclones must be driven by convection:

One other note:

The rate of heat transfer from the warm surface ocean, to the atmosphere, in a developing tropical cyclone, is mostly dependent on the surface wind speed.