
Since numerical examples are often useful to show various scalings let's do another one:
The first law of Thermodynamics can be expressed in many forms.
If we work in units of specific volume (α) we can express
the first law as:
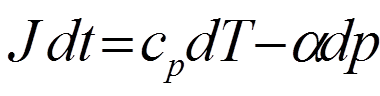
Where J represents what is called the DIABATIC heating rate in
units of Joules kg -1 s-1. The diabatic heating concerns temperature changes that are NOT related to vertical displacement of air.
Dividing through by dt and rearranging terms yields:
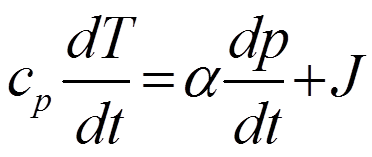
Now we divide through by cp and use the ideal gas law in the form p = αRT and then define ω = dp/dt
we get
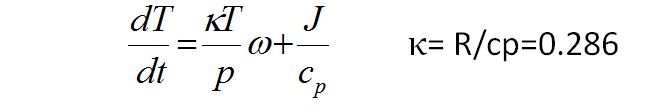
which is known as the Thermodynamic Energy Equation
The first term in this equation is the rate of change of temperature due to adiabatic expansion or compression and NOT displacement.
The second term represents the effects of DIABATIC heat sources
and sinks. These include
- Absorption of short wavelength incoming solar radiation
- Absorption and/or emission of long wavelength radiation
- latent heat release
- heat absorbed or liberated in chemical reactions (this is the source of heating in the ozone layer)
- Exchange of mass with the Environment through convection
and turbulence.
Observationally we know that the second term is less than 1 degree per day. This is just a statement that on large scales,
the various heat exchange mechanisms are pretty much in equilibrium.
In turn, this means that the primary heating of a parcel of air is the result of its vertical motion.
We can estimate the magnitude of the first term as follows:
|