An Ekman current is essentially a balance between the Coriolis force and frictional forces where the frictional force is the result of VERTICAL mixing (involving "parcels" of water with different temperatures, salinities and densities) of momentum.
The vertical rate of momentum mixing is Az the eddy viscosity profile.
This current then gives rise to Ekman transport which is essentially the mass transport per meter that is perpendicular to the Ekman Spiral (see the You Tube Videos). That transport is in units of m2 s-1 and is essentially:
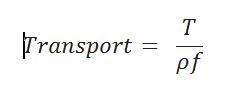
(remember T is wind stress, essentially wind velocity).
Upwelling:
Since the ocean is not infinite and winds are highly variable, Ekman transports are not spatially uniform and this leads to convergence and divergence of surface ocean currents.
The best example of this is characteristic upwelling at coastlines. Winds blowing parallel to the coasdt obviously can not drive Ekman tranport across the coastline because there is no fluid. So what happens?  a strong vertical velocity develops in the Ekman current bringing deep water (or water down to the Ekman depth ~200 m) to the surface.
On say the California coast, the prevailing wind is from the North which dives Ekman tranport OFF shore and this water must be replaced (mass continuity) by upwelling.
The zone of active upwelling is usually manifest as a band of wold water adjacent to the coast. This band has a characteristic width detemined by the equivalient Rossby radius (this is an upwelling vortex). We can make a simple estimate of this width and compare that to real world values.
Rossby Radius = c/f ; c = wave speed; f = coriolis
c = √g'h
g'=g(δρ/ρ)
R = √gh(δρ/ρ)*f-1
Well, California example
- h = average depth ~ 100 m
- (δρ) ~2 kg m-3
- ρ = 1025 kg m-3
- f = 10-4 s-1 (at 40 degrees latitude)
- g = 10
R ~ 14 km
Off the coast of Peru at 10 degrees latitude f ~ 10-5 s-1 and h ~ 300m so R ~240 km!
|