Derivation of exponential exhaustion time scale: requires calculus

Some Notes on exponential growth:

1) Its very likely that you have been erroneously exposed to exponential growth. Exponential growth does not necessarily imply unbounded growth. Thus the human population can continue to grow exponentially, but not necessarily unbounded. Indeed, that is the current trajectory - human population grows exponentially but the rate of growth declines every year. The waveform of that kind of exponential growth is shown here with respect to world population:

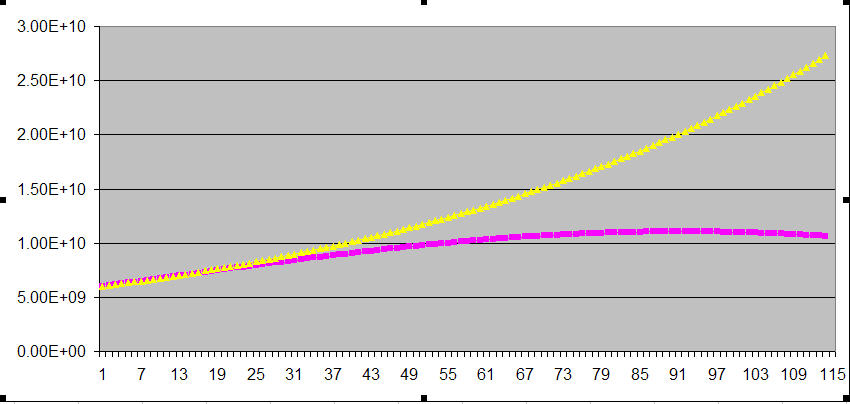
• The yellow curve represents the case of exponential growth at a constant rate (in this case 1.35% per year which was the growth rate in the year 2000).
  
  
  
• The Pink curve represents the case of exponential growth at a rate that declines at .05% per year which is the likely trajectory of human population growth. Mathematically, this eventually leads to negative population growth - but the point remains - the pink curve is still defined by exponential functions!
  
  
  

2) how to calculate an exponential doubling time ( Derivation here )

3) how to determine exponential growth from the data themselves: Its pretty simple. Take the natural log of the ratio of the final population to the initial population and divide that by the number of years between the initial and final populations.

Example (pop growth in california):

• Population in 1980 = 23.7 million
• Population in 1993 (14 years later) = 31.2 million
• ratio of final to initial population is 31.2/23.7 = 1.32
• Natural Log of 1.32 (ln 1.32) = 0.28
• 0.28/14 = 0.02 (2% annual growth rate)